【题目】⊙O的半径为13cm,AB,CD是⊙O的两条弦,AB∥CD,AB=24cm,CD=10cm.则AB和CD之间的距离 .
参考答案:
【答案】7cn或17cm
【解析】解:作OE⊥AB于E,交CD于F,连结OA、OC,如图,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE= ![]() AB=12,CF=DF=
AB=12,CF=DF= ![]() CD=5,
CD=5,
在Rt△OAE中,∵OA=13,AE=12,
∴OE= ![]() =5,
=5,
在Rt△OCF中,∵OC=13,CF=5,
∴OF= ![]() =12,
=12,
当圆心O在AB与CD之间时,EF=OF+OE=12+5=17;
当圆心O不在AB与CD之间时,EF=OF﹣OE=12﹣5=7;
即AB和CD之间的距离为7cn或17cm.
所以答案是7cn或17cm.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的解析式为y=ax2+bx+c,则下列说法中错误的是( )
A.a确定抛物线的形状与开口方向
B.若将抛物线C沿y轴平移,则a,b的值不变
C.若将抛物线C沿x轴平移,则a的值不变
D.若将抛物线C沿直线l:y=x+2平移,则a、b、c的值全变 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的解析式为y=ax2+bx+c(a、b、c为常数,a≠0),且a2+ab+ac<0,下列说法:
①b2﹣4ac<0;
②ab+ac<0;
③方程ax2+bx+c=0有两个不同根x1、x2 , 且(x1﹣1)(1﹣x2)>0;
④二次函数的图象与坐标轴有三个不同交点,
其中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )
A.
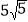 cm B.
cm B. 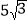 cm C. 12cm D. 13cm
cm C. 12cm D. 13cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△OBA,∠ABO=30°,OA=2,两条直角边重叠在互相的垂直的两条直线上,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在直线AO上运动,如果PQ=
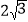 ,那么当点P运动一周时,点Q运动的总路程为____________.
,那么当点P运动一周时,点Q运动的总路程为____________.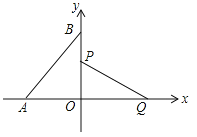
-
科目: 来源: 题型:
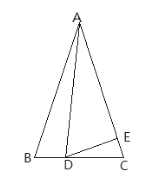
查看答案和解析>>【题目】如图,已知在△ABC中,∠ABC=65°,AB=AC,∠BAD=20°,AD=AE,求∠EDC的度数.
相关试题

