搜索
【题目】已知等腰三角形三条边的长分别为
、
、
，若
，、是关于
的方程
的两个根，则
的值为______．
参考答案：
【答案】12或16
【解析】
根据根与系数的关系可得出b+c=8、bc=m，分a=6为腰长或a=6为底长两种情况考虑：当a=6为腰长时，可得出b、c的长度，进而可得出m的值，利用三角形的三边关系验证后可得出m=12符合题意；当a=6为底长时，根据等腰三角形的性质可得出b、c的长度，进而可得出m的值，利用三角形的三边关系验证后可得出m=16符合题意．此题得解．
解：∵b、c是关于x的方程x2-8x+m=0两个根，
∴b+c=8，bc=m．
当a=6为腰长时，b=6，c=2，此时m=12（或c=6，b=2，m=12），
∵6，6，2可组成等腰三角形，
∴m=12符合题意；
当a=6为底长时，∵b+c=8，b=c，
∴b=c=4，
∴m=16，
∵6，4，4可组成等腰三角形，
∴m=16符合题意．
故答案为：12或16．
-
科目： 来源： 题型：
查看答案和解析>>【题目】张师傅开车到某地送货，汽车出发前油箱中有油50升，行驶一段时间，张师傅在加油站加油，然后继续向目的地行驶．已知加油前、后汽车都匀速行驶，汽车行驶时每小时的耗油量一定．油箱中剩余油量Q（升）与汽车行驶时间t（时）之间的函数图象如图所示．
（1）张师傅开车行驶________小时后开始加油，本次加油________升．
（2）求加油前Q与t之间的函数关系式．
（3）如果加油站距目的地210千米，汽车行驶速度为70千米/时，张师傅要想到达目的地，油箱中的油是否够用？请通过计算说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：在三角形中，把一边的中点到这条边的高线的距离叫做这条边的中垂距．
例：如图①，在△ABC中，D为边BC的中点，AE⊥BC于E，则线段DE的长叫做边BC的中垂距．
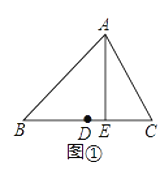
（1）设三角形一边的中垂距为d（d≥0）．若d=0，则这样的三角形一定是________，推断的数学依据是________．
（2）如图②，在△ABC中，∠B=45°，AB=
，BC=8，AD为边BC的中线，求边BC的中垂距．
（3）如图③，在矩形ABCD中，AB=6，AD=4．点E为边CD的中点，连结AE并延长交BC的延长线于点F，连结AC．求△ACF中边AF的中垂距．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，AB=BC=6，∠B=60°，∠D=90°，连结AC．动点P从点B出发，沿BC以每秒1个单位的速度向终点C运动（点P不与点B、C重合）．过点P作PQ⊥BC交AB或AC于点Q，以PQ为斜边作Rt△PQR，使PR∥AB．设点P的运动时间为t秒．
（1）当点Q在线段AB上时，求线段PQ的长．（用含t的代数式表示）
（2）当点R落在线段AC上时，求t的值．
（3）设△PQR与△ABC重叠部分图形的面积为S平方单位，求S与t之间的函数关系式．
（4）当点R到C、D两点的距离相等时，直接写出t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们约定：体重在选定标准的
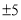%（包含）范围之内时都称为“一般体重”．为了解某校七年级男生中具有“一般体重”的人数，我们从该校七年级男生中随机选出10名男生，测量出他们的体重（单位：kg），收集并整理得到如下统计表：男生序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
体重
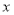（kg）45
62
55
58
67
80
53
65
60
55
根据以上表格信息解决如下问题:
（1）将这组数据的三个统计量：平均数、中位数和众数填入下表：
平均数
中位数
众数
（2）请你选择其中一个统计量作为选定标准，说明选择的理由．并按此选定标准找出这10名男生中具有“一般体重”的男生．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于
的一元二次方程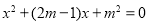
有两个实数根
，
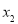．（1）分别用含
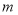的代数式表示
，
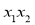的值．（2）若
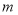，求的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线y=﹣x+3与抛物线
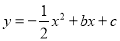交于A、B两点，点A在x轴上，点B的横坐标为
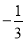．动点P在抛物线上运动（不与点A、B重合），过点P作y轴的平行线，交直线AB于点Q．当PQ不与y轴重合时，以PQ为边作正方形PQMN，使MN与y轴在PQ的同侧，连结PM．设点P的横坐标为m．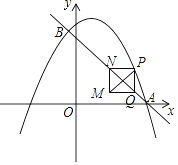
（1）求b、c的值．
（2）当点N落在直线AB上时，直接写出m的取值范围．
（3）当点P在A、B两点之间的抛物线上运动时，设正方形PQMN的周长为C，求C与m之间的函数关系式，并写出C随m增大而增大时m的取值范围．
（4）当△PQM与坐标轴有2个公共点时，直接写出m的取值范围．
相关试题
