【题目】张师傅开车到某地送货,汽车出发前油箱中有油50升,行驶一段时间,张师傅在加油站加油,然后继续向目的地行驶.已知加油前、后汽车都匀速行驶,汽车行驶时每小时的耗油量一定.油箱中剩余油量Q(升)与汽车行驶时间t(时)之间的函数图象如图所示.

(1)张师傅开车行驶________小时后开始加油,本次加油________升.
(2)求加油前Q与t之间的函数关系式.
(3)如果加油站距目的地210千米,汽车行驶速度为70千米/时,张师傅要想到达目的地,油箱中的油是否够用?请通过计算说明理由.
参考答案:
【答案】(1)3;31;(2)Q=﹣12t+50(0≤t≤3);(3)张师傅要想到达目的地,油箱中的油够用.
【解析】试题分析:(1)观察函数图象可知张师傅开车行驶3小时后开始加油,由加油后的剩余油量-加油前的剩余油量=加油量,即可求出本次加油的升数。
(2)观察函数图象找出两点的坐标,利用待定系数法即可求出加油前Q与t之间的函数关系式。
(3)先求出每小时的耗油量,再求出到达目的地还需耗油量,将其与油箱中剩余油量比较后即可得出结论。
(1)观察函数图象可知:张师傅开车行驶3小时后开始加油,45﹣14=31(升).
(2)解:设加油前Q与t之间的函数关系式为Q=kt+b(k≠0),
将(0,50)、(3,14)代入Q=kt+b,
得: ![]() ,
,
解得: ![]() ,
,
加油前Q与t之间的函数关系式为Q=﹣12t+50(0≤t≤3)
(3)解:该车每小时耗油量为:(50﹣14)÷3=12(升),
∴到达目的地还需耗用12×(210÷70)=36(升),
∵45>36,
∴张师傅要想到达目的地,油箱中的油够用
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
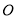 是正
是正 内一点,
内一点,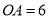 ,
, ,
, ,将线段
,将线段 以点
以点 为旋转中心逆时针旋转
为旋转中心逆时针旋转 得到线段
得到线段 ,下列结论:①
,下列结论:①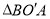 可以由
可以由 绕点
绕点 逆时针旋转
逆时针旋转 得到;②点
得到;②点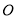 与点
与点 的距离为8;③
的距离为8;③ ;④
;④ ;其中正确的结论是( )
;其中正确的结论是( )
A.①②③B.①③④C.②③④D.①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某商场计划购进一批
 、
、 两种空气净化装置,每台
两种空气净化装置,每台 种设备价格比每台
种设备价格比每台 种设备价格多0.7万元,花3万元购买
种设备价格多0.7万元,花3万元购买 种设备和花7.2万元购买
种设备和花7.2万元购买 种设备的数量相同.
种设备的数量相同.(1)求
 种、
种、 种设备每台各多少万元?
种设备每台各多少万元?(2)根据销售情况,需购进
 、
、 两种设备共20台,总费用不高于15万元,求
两种设备共20台,总费用不高于15万元,求 种设备至少要购买多少台?
种设备至少要购买多少台?(3)若每台
 种设备售价0.6万元,每台
种设备售价0.6万元,每台 种设备售价1.4万元,在(2)的情况下商场应如何进货才能使这批空气净化装置售完后获利最多?
种设备售价1.4万元,在(2)的情况下商场应如何进货才能使这批空气净化装置售完后获利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
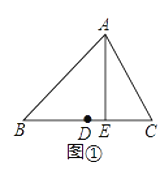
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是________,推断的数学依据是________.
(2)如图②,在△ABC中,∠B=45°,AB=
 ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AB=BC=6,∠B=60°,∠D=90°,连结AC.动点P从点B出发,沿BC以每秒1个单位的速度向终点C运动(点P不与点B、C重合).过点P作PQ⊥BC交AB或AC于点Q,以PQ为斜边作Rt△PQR,使PR∥AB.设点P的运动时间为t秒.

(1)当点Q在线段AB上时,求线段PQ的长.(用含t的代数式表示)
(2)当点R落在线段AC上时,求t的值.
(3)设△PQR与△ABC重叠部分图形的面积为S平方单位,求S与t之间的函数关系式.
(4)当点R到C、D两点的距离相等时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形三条边的长分别为
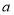 、
、 、
、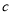 ,若
,若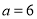 ,
, 、
、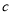 是关于
是关于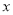 的方程
的方程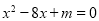 的两个根,则
的两个根,则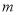 的值为______.
的值为______.
相关试题

