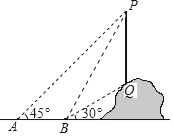
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
A. 6+2![]() B. 6+
B. 6+![]() C. 10﹣
C. 10﹣![]() D. 8+
D. 8+![]()
参考答案:
【答案】A
【解析】
延长PQ交直线AB于点E,设PE=xm,在Rt△APE和Rt△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,然后在Rt△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
解:延长PQ交直线AB于点E,设PE=xm.
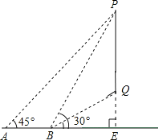
在Rt△APE中,∠A=45°,
则AE=PE=xm,
∵∠PBE=60°,
∴∠BPE=30°,
在Rt△BPE中,
BE=![]() PE=
PE=![]() xm,
xm,
∵AB=AEBE=6m,
则x![]() x=6,
x=6,
解得:x=9+3![]() ,
,
∴BE=3![]() +3 (m),
+3 (m),
在Rt△BEQ中,
QE=![]() BE=
BE=![]() (3
(3![]() +3)= 3+
+3)= 3+![]() (m),
(m),
∴PQ=PEQE=9+3![]() (3+
(3+![]() )=6+2
)=6+2![]() (m).
(m).
故选A.
-
科目: 来源: 题型:
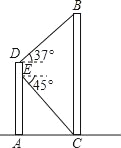
查看答案和解析>>【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
-
科目: 来源: 题型:
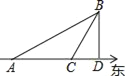
查看答案和解析>>【题目】如图,某船于上午11时30分在A处观察海岛B在北偏东60°,该船以10海里/小时的速度向东航行至C处,再观察海岛在北偏东30°,且船距离海岛20海里.
(1)求该船到达C处的时刻.
(2)若该船从C处继续向东航行,何时到达B岛正南的D处?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在斜坡EF上有一信号发射塔CD,某兴趣小组想要测量发射塔CD的高度,于是在水平地面用仪器测得塔顶D的仰角为31°,已知仪器AB高为2m,斜坡EF的坡度为i=3:4,塔底距离坡底的距离CE=10m,最后测得塔高为12m,A、B、C、D、E在同一平面内,则仪器到坡底距离AE约为( )米(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)

A. 18.6 B. 18.7 C. 22.0 D. 24.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=
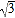 米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).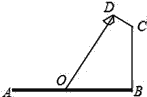
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为
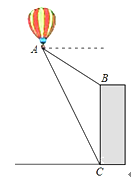 ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为 ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米

相关试题

