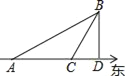
【题目】如图,某船于上午11时30分在A处观察海岛B在北偏东60°,该船以10海里/小时的速度向东航行至C处,再观察海岛在北偏东30°,且船距离海岛20海里.
(1)求该船到达C处的时刻.
(2)若该船从C处继续向东航行,何时到达B岛正南的D处?
参考答案:
【答案】解:∵∠BAC=30o,∠BCD=60o
∴∠CBA=30o
∴AC=BC=40
∴A到达C点所用的时间为40/10=4(小时)
∴船到达C点的时间是15:30
(2)在直角三角形ABD中,∠A=30o,
∴∠ABD=60o,
又∵∠CBA=30o
∴∠CBD=30o
∴CD=1/2BC=20
∴C到达D点所用的时间为20/10=2(小时)
∴船到达D点的时间是17:30
【解析】
(1)根据题意得:∠A=30°,∠BCD=60°,BC=40海里,根据三角形外角的性质,易证得∠ABC=∠A,根据等角对等边,即可求得AC=BC,又由船的速度为10海里/时,即可求得船到达C点的时间;
(2)由在Rt△BCD中,∠BCD=60°,BC=40海里,即可求得CD的长,继而求得到达B岛正南的D处的时间.
-
科目: 来源: 题型:
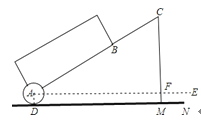
查看答案和解析>>【题目】一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,⊙A与水平地面切于点D,AE∥DN,某一时刻,点B距离水平面38cm,点C距离水平面59cm.
(1)求圆形滚轮的半径AD的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面73.5cm,求此时拉杆箱与水平面AE所成角∠CAE的大小(精确到1°,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
-
科目: 来源: 题型:
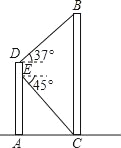
查看答案和解析>>【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
-
科目: 来源: 题型:
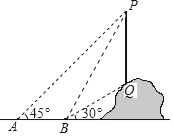
查看答案和解析>>【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
A. 6+2
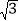 B. 6+
B. 6+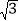 C. 10﹣
C. 10﹣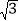 D. 8+
D. 8+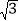
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在斜坡EF上有一信号发射塔CD,某兴趣小组想要测量发射塔CD的高度,于是在水平地面用仪器测得塔顶D的仰角为31°,已知仪器AB高为2m,斜坡EF的坡度为i=3:4,塔底距离坡底的距离CE=10m,最后测得塔高为12m,A、B、C、D、E在同一平面内,则仪器到坡底距离AE约为( )米(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)

A. 18.6 B. 18.7 C. 22.0 D. 24.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=
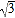 米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).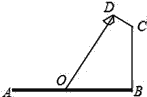
相关试题

