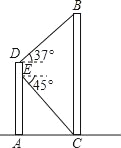
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
参考答案:
【答案】解:过点E、D分别作BC的垂线,交BC于点F、G.
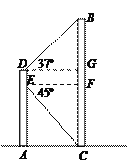
在Rt△EFC中,因为FC=AE=20,∠FEC=45°
所以EF=20 ………2分
在Rt△DBG中,DG=EF=20,∠BDG=37°
因为tan∠BDG=![]() ≈0.75 ………4分
≈0.75 ………4分
所以BG≈DG×0.75=20×0.75=15………5分
而GF=DE=5所以BC=BG+GF+FC=15+5+20=40
答:大楼BC的高度是40米. ………6分
【解析】
首先过点E、D分别作BC的垂线,交BC于点F、G,得两个直角三角形△EFC和△BDG,由已知大楼BC楼底C点的俯角为45°得出EF=FC=AE=20,DG=EF=20,再由直角三角形BDG,可求出BG,GF=DE=5,CO从而求出大楼的高度BC.
过点E、D分别作BC的垂线,交BC于点F、G.

在Rt△EFC中,因为FC=AE=20,∠FEC=45°
所以EF=20
在Rt△DBG中,DG=EF=20,∠BDG=37°
因为tan∠BDG=![]() ≈0.75
≈0.75
所以BG≈DG×0.75=20×0.75=15
而GF=DE=5
所以BC=BG+GF+FC=15+5+20=40
答:大楼BC的高度是40米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
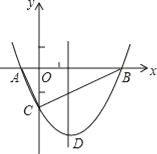
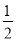 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是
 的直径,点C、D在
的直径,点C、D在 上,且AD平分
上,且AD平分 ,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB. 证明EF是
证明EF是 的切线;
的切线; 求证:
求证: ;
; 已知圆的半径
已知圆的半径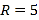 ,
,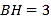 ,求GH的长.
,求GH的长.
-
科目: 来源: 题型:
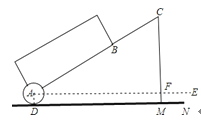
查看答案和解析>>【题目】一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,⊙A与水平地面切于点D,AE∥DN,某一时刻,点B距离水平面38cm,点C距离水平面59cm.
(1)求圆形滚轮的半径AD的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面73.5cm,求此时拉杆箱与水平面AE所成角∠CAE的大小(精确到1°,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
-
科目: 来源: 题型:
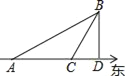
查看答案和解析>>【题目】如图,某船于上午11时30分在A处观察海岛B在北偏东60°,该船以10海里/小时的速度向东航行至C处,再观察海岛在北偏东30°,且船距离海岛20海里.
(1)求该船到达C处的时刻.
(2)若该船从C处继续向东航行,何时到达B岛正南的D处?
-
科目: 来源: 题型:
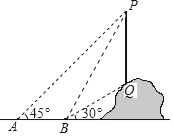
查看答案和解析>>【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
A. 6+2
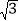 B. 6+
B. 6+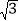 C. 10﹣
C. 10﹣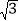 D. 8+
D. 8+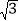
相关试题

