【题目】关于x的方程(k﹣1)x2+2kx+2=0.
(1)求证:无论k为何值,方程总有实数根.
(2)设x1,x2是方程(k﹣1)x2+2kx+2=0的两个根,记![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
参考答案:
【答案】(1)见解析;(2) k=2
【解析】试题分析:
(1)①当k=1时,原方程是一元一次方程,其有解;②当![]() 时,原方程是一元二次方程,列出“根的判别式的表达式”,并证明其值为非负数即可可得出原方程一定有实数根;综合①②可得结论;
时,原方程是一元二次方程,列出“根的判别式的表达式”,并证明其值为非负数即可可得出原方程一定有实数根;综合①②可得结论;
(2)由原方程有两根可知:“![]() ”,根据“一元二次方程根与系数的关系”列出“两根和与两根积的表达式”代入S=2中得到关于“k”的方程,解方程求出“k”的值即可.
”,根据“一元二次方程根与系数的关系”列出“两根和与两根积的表达式”代入S=2中得到关于“k”的方程,解方程求出“k”的值即可.
试题解析:
(1)①当k=1时,原方程可化为2x+2=0,解得:x=﹣1,此时该方程有实根;
②当k≠1时,方程是一元二次方程,
∵△=(2k)2﹣4(k﹣1)×2
=4k2﹣8k+8
=4(k﹣1)2+4>0,
∴无论k为何实数,方程总有实数根;
综上所述,无论k为何实数,方程总有实数根.
(2)∵原方程有两根实数根,
∴原方程为一元二次方程, ![]() .
.
由根与系数关系可知, ![]() ,
, ![]() ,
,
若S=2,则![]() ,即
,即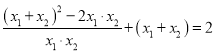 ,
,
将![]() ,
, ![]() 代入整理得:
代入整理得: ![]() ,
,
解得:k=1(舍)或k=2,
∴S的值能为2,此时k=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a3﹣a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.
(1)求证:AB为⊙C直径.
(2)求⊙C的半径及圆心C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算:ab=a(1﹣b).若a,b是方程x2﹣x+
 m=0(m<0)的两根,则bb﹣aa的值为( )
m=0(m<0)的两根,则bb﹣aa的值为( )A. 0 B. 1 C. 2 D. 与m有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然事件的个数为( )
①标准大气压下,水加热到100 ℃沸腾;②某种彩票中奖的概率是1%,买100张该种彩票会中奖;③任意投掷一枚质地均匀的硬币,正面朝上;④367人中至少有两人的生日相同.
A. 1 B. 2 C. 3 D. 4
相关试题

