【题目】如图,直线AB与CD相交于点O,∠AOE=∠DOF=90°,OP是∠BOC的平分线,∠AOD=40°.
(1)求∠EOP的度数;
(2)写出∠AOD的补角和余角.

参考答案:
【答案】(1) 70°;(2)∠AOD的补角:∠AOC,∠BOD和∠EOF;∠AOD的余角:∠COE和∠BOF.
【解析】(1)由对顶角相等可求∠BOC=∠AOD=40°,由角平分线可求∠BOP=20°,然后根据∠EOP=∠EOB-∠BOP可求结论;
(2)根据补角和余角的定义求解即可.
(1)因为∠AOD=40°,
所以∠BOC=40°.
因为OP是∠BOC的平分线,
所以∠BOP=![]() ∠BOC=20°,
∠BOC=20°,
所以∠EOP=∠EOB-∠BOP=70°.
(2)∠AOD的补角:∠AOC,∠BOD和∠EOF;
∠AOD的余角:∠COE和∠BOF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )

A. a2-b2=(a+b)(a-b) B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. a2-ab=a(a-b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( )
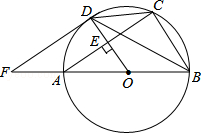
A.∠CDB=∠BFD
B.△BAC∽△OFD
C.DF∥AC
D.OD=BC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )

A.
B.
C.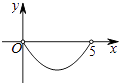
D.
-
科目: 来源: 题型:
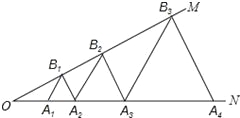
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为 .
相关试题

