【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
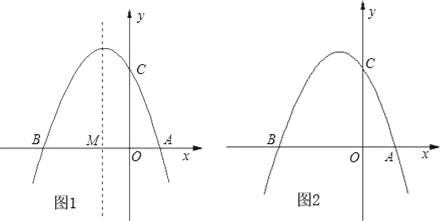
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
参考答案:
【答案】解:(1)![]()
(2)存在P1(-1, ![]() )、P2(1,6),P3(1,
)、P2(1,6),P3(1, ![]() )
)
(3)连OE设四边形BOCE的面积为S,点E的坐标为(![]() )
)
∵E在第二象限
∴3<x<0 -x2-2x+3>0
∵S=S△BOE+S△COE=![]() +
+![]() ×3×(-×)
×3×(-×)
=![]()
∵-3<x<0
∴当x=-![]() 时,S最大为
时,S最大为![]()
此时,E(![]() )
)
【解析】试题分析:(1)利用待定系数法求函数解析式即可;(2)分CP=MP、CM=CP、CM=MP三种情况讨论,(3)过点E作EF⊥x轴于点F,设E(a,-![]() -2a+3)(-3<a<0),然后用a表示出四边形BOCE面积,然后利用二次函数的性质确定最大值即可得到点E坐标.
-2a+3)(-3<a<0),然后用a表示出四边形BOCE面积,然后利用二次函数的性质确定最大值即可得到点E坐标.
试题解析:解︰(1)由题知︰![]() ,解得︰
,解得︰![]()
∴所求抛物线解析式为︰![]()
(2)存在符合条件的点P,
其坐标为P(-1,![]() )或P(-1,-
)或P(-1,-![]() )或P(-1,6)或P(-1,
)或P(-1,6)或P(-1,![]() )
)
(3)解法①:
过点E作EF⊥x轴于点F,设E(a,-![]() -2a+3)(-3<a<0)
-2a+3)(-3<a<0)
∴EF=-![]() -2a+3,BF=a+3,OF=-a
-2a+3,BF=a+3,OF=-a
∴S四边形BOCE=![]() BF·EF+
BF·EF+![]() (OC+EF)·OF
(OC+EF)·OF
=![]() (a+3)·(-
(a+3)·(-![]() -2a+3)+
-2a+3)+![]() (-
(-![]() -2a+6)·(-a)
-2a+6)·(-a)
=![]() =-
=-![]()
![]() +
+![]()
∴当a=-![]() 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为![]() .
.
此时,点E坐标为(-![]() ,
,![]() )
)
解法②:
过点E作EF⊥x轴于点F,设E(x,y)(-3<x<0)
则S四边形BOCE=![]() (3+y)·(-x)+
(3+y)·(-x)+![]() (3+x)·y
(3+x)·y
=![]() (y-x)=
(y-x)=![]() (
(![]() )=-
)=-![]()
![]() +
+![]()
∴当x=-![]() 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为![]() .此时,点E坐标为(-
.此时,点E坐标为(-![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个单项式加上多项式x2﹣6x+4后等于一个整式的平方,试求这样的单项式并写出相应的等式(请写3个)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC、BD相交于点O,

(1)若AB=4cm,AD=8cm,当BC=cm,CD=cm时,四边形ABCD为平行四边形;
(2)若BD=8cm,AC=10cm,当AO=cm,DO=cm时,四边形ABCD为平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(a﹣1)(a+1)﹣(a﹣1)2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是 . (添加一个条件即可,不添加其它的点和线).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列(a+3)(b﹣4)的展开式中正确的是( )
A.ab﹣4b+3a﹣12
B.ab﹣4a+3b﹣12
C.ab﹣4b+3a+12
D.ab﹣4a+3b+12. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
A. 40° B. 60° C. 80° D. 90°
相关试题

