【题目】在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)若从盒子里随机摸出一只球,则摸到白球的概率的估计值为 ;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
参考答案:
【答案】(1)0.6;(2)0.6;(3)盒子里黑、白两种颜色的球各有16只, 24只.
【解析】试题分析:⑴ 观察图表可知,当![]() 很大时,摸到白球的频率接近0.6 .
很大时,摸到白球的频率接近0.6 .
⑵ 当实验次数很大时,频率接近概率,所以摸到白球的概率估值为0.6 .
⑶ 摸到白球概率为0.6,摸到黑球的概率为0.4,那么白球数量为![]() 个,
个,
黑球数量为![]() 个.
个.
试题解析:(1)∵摸到白球的频率为0.6,
∴当n很大时,摸到白球的频率将会接近0.6,
故答案为:0.6;
(2)∵摸到白球的频率为0.6,
∴假如你摸一次,你摸到白球的概率P(白球)=0.6,
故答案为:0.6;
(3)盒子里黑、白两种颜色的球各有40﹣24=16,40×0.6=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县政府打算用25000元用于为某乡福利院购买每台价格为2000元的彩电和每台价格为1800元的冰箱,并计划恰好全部用完此款.
(1)问原计划所购买的彩电和冰箱各多少台?
(2)由于国家出台“家电下乡”惠农政策,该县政府购买的彩电和冰箱可获得13%的财政补贴,若在不增加县政府实际负担的情况下,能否多购买两台冰箱?谈谈你的想法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国汉代数学家赵爽为了证明勾股定理,创造了一幅“弦图”后人称其为“赵爽弦图”(如图1).图2是弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,求S2的值.以下是求S2的值的解题过程,请你根据图形补充完整.
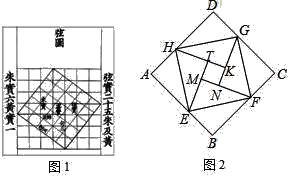
解:设每个直角三角形的面积为S
S1﹣S2= (用含S的代数式表示)①
S2﹣S3= (用含S的代数式表示)②
由①,②得,S1+S3= 因为S1+S2+S3=10,
所以2S2+S2=10.
所以S2=
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了了解七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查。根据收集的数据绘制了下面的频数分市直方图,则以下说法正确的是( )

A. 绘制该频数分布直方图时选取的组距为10分成的组数为5
B. 这50人中大多数学生参加社会实践活动的时间是12-14h
C. 这50人中有64%的学生参加社会实践活动时间不少于10h
D. 可以估计全年级700人中参加社会实践活动时间为6~8h的学生大约为28人
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(1)当∠E=∠F时,则∠ADC=_____°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中, D,E,F三点分别在AB,AC,BC上,过点D的直线与线段EF的交点为点M,已知2∠1-∠2=150°,2∠ 2-∠1=30°.
(1)求证:DM∥AC;
(2)若DE∥BC,∠C =50°,求∠3的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算、求解:
(1)用代人消元法解方程组:
 ;
;(2)加减消元法解方程组:
 ;
;(3)计算:
 ;
;(4)解不等式组
 ,并把解集在数轴上表示出来,
,并把解集在数轴上表示出来,
相关试题

