搜索
【题目】给出下列命题：①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；②三角形的三边a、b、c满足a2+c2＝b2，则∠C＝90°；③△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC是直角三角形；④△ABC中，若a：b：c＝1：2：
，则这个三角形是直角三角形，其中，正确命题为_____（选填序号）．
参考答案：
【答案】③④
【解析】
根据勾股定理、三角形内角和定理、勾股定理的逆定理判断．
解：①在直角三角形
中，已知两边长为3和4，
当4是直角边时，第三边
，
当4是斜边长时，第三边
则第三边长为5或
，本说法是假命题；
②三角形的三边
、
、
满足
，则
，本说法是假命题；
③
中，若
，
设
、
、
分别为
、
、
，
则
，
解得，
，
则、、分别为
、
、
，
则是直角三角形，本说法是真命题；
④中，若
，
设、、分别为、
、
，
，
，
，
这个三角形是直角三角形，本说法是真命题，
故答案为：③④．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC的周长是20，OB和OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD=3，则△ABC的面积是（ ）
A. 20 B. 25 C. 30 D. 35
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC＝2，∠BAC＝30°，则线段PM的最大值是（ ）
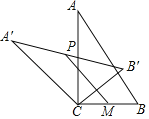
A.4B.3C.2D.1
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
与坐标轴分别交于点A、点B、点C,并且∠ACB=90,AB=10.(1)求证:△OAC∽△OCB;
(2)求该抛物线的解析式；
(3)若点P是(2)中抛物线对称轴上的一个动点,是否存在点P使得△PAC为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD，CE相交于F.
求证：AF平分∠BAC.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A、B、C、D的坐标分别是（1，7），（1，1），（4，1），（6，1），以C、D、E为顶点的三角形与△ABC相似，则点E的坐标不可能是（ ）
A．（4，2） B．（6，0） C．（6，3） D．（6，5）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣
（x+1）（x﹣3）与x轴交于A、B两点，与y轴交于点C，点D为该抛物线的对称轴上一点，当点D到直线BC和到x轴的距离相等时，则点D的坐标为 ．
相关试题
