搜索
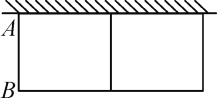
【题目】如图，为了美化街道，刘大爷准备利用自家墙外的空地种植两种不同的花卉，墙的最大可用长度是12.5m，墙外可用宽度为3.25m．现有长为21m的篱笆，计划靠着院墙围成一个中间有一道隔栏的长方形花圃．
(1)若要围成总面积为36m2的花圃，边AB的长应是多少？
(2)花圃的面积能否达到36.75m2？若能，求出边AB的长；若不能，请说明理由．
参考答案：
【答案】（1）x只能取3；（2）花圃的面积不能达到36.75m2
【解析】
（1）设AB的长为x米，则长为21-3x米，根据其面积列出方程求得即可．
（2）把（1）中用代数式表示的面积整理为a（x-h）2+b的形式可得最大的面积．
（1）设AB的长为x米，则长为（21-3x）米，
根据题意得：x（21-3x）=36，
解得：x=3或x=4，
∵墙外可用宽度为3.25m，
∴x只能取3．
（2）花圃的面积为（21-3x）x=-3（x-3.5）2+36.75，
∴当AB长为3.5m，有最大面积，为36.75平方米．
因为3.5>3.25故花圃的面积不能达到36.75m2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知∠ABC=
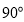,D是直线AB上的一点，AD=BC，连结DC.以DC为边，在∠CDB的同侧作∠CDE，使得∠CDE=∠ABC，并截取DE=CD，连结AE.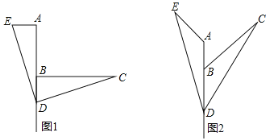
(1)求证:
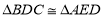;并判断AE和BC的位置关系，说明理由；(2)若将题目中的条件“∠ABC=900”改成“∠ABC=x0(0<x<180)”,
①结论“
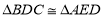”还成立吗?请说明理由；②试探索:当
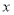的值为多少时，直线AE⊥BC. -
科目： 来源： 题型：
查看答案和解析>>【题目】2018年12月4日是第五个国家宪法日，也是第一个“宪法宣传周”．甲、乙两班各选派10名学生参加宪法知识竞赛（满分100分），成绩如下：
成绩
85
90
95
100
甲班参赛学生/人
1
1
5
3
乙班参赛学生/人
1
2
3
4
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在 ABCD 中，AE、BF 分别平分∠DAB 和∠ABC，交 CD 于点 E、F，AE、BF 相交于点 M．
（1）求证：AE⊥BF；
（2）判断线段 DF 与 CE 的大小关系，并予以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为迎接五一国际劳动节，某校团委组织了“劳动最光荣”有奖征文活动，并设立了一、二、三等奖．学校计划派人根据设奖情况买50件奖品，其中二等奖件数比一等奖件数的2倍还少10件，三等奖所花钱数不超过二等奖所花钱数的1.5倍．各种奖品的单价如下表所示．如果计划一等奖买x件，买50件奖品的总钱数是w元．
（1）求w与x的函数关系式及自变量
的取值范围；（2）请你计算一下，如何购买这三种奖品所花的总钱数最少？最少是多少元？
一等奖
二等奖
三等奖
12元
10元
5元
-
科目： 来源： 题型：
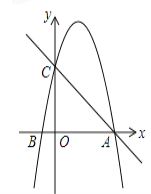
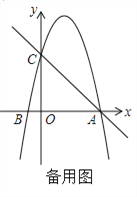
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A 的坐标是(4,0)，并且0A=OC=4OB,动点P在过A,B，C三点的抛物线上.
(1) 求抛物线的解析式;
(2)过动点P作PE垂直于y轴于点E,交直线AC于点D，过点D作x轴的垂线，垂足为F,连接EF,当线段EF的长度最短时，求出点P的坐标;
(3) 是否存在点P,使得△ACP是以AC为直角边的直角三角形? 若存在，求出所有符合条件的点P的坐标; 若不存在，说明理由
-
科目： 来源： 题型：
查看答案和解析>>【题目】解不等式(组)或方程(组)：
（1）
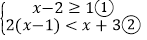（2）
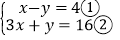
（3）(x－5)(x＋4)＝10；（4）
.
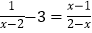相关试题
