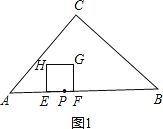
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.

(1)当t=1时,正方形EFGH的边长是 ;当t=4时,正方形EFGH的边长是 ;
(2)当0<t≤3时,求S与t的函数关系式.
参考答案:
【答案】(1)3; 8. (2)S=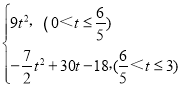 .
.
【解析】
试题分析:(1)当t=1时,根据PE=2t,PF=t即可求出EF的值,当t=4时,点E运动到点A后返回,PE=2AP-2t,PF=t,由此即可求出EF的值;
(2)当点H在线段AC上时,可求出t=![]() ,可分两种情况讨论:当0<t≤
,可分两种情况讨论:当0<t≤![]() 时,S=S正方形EFGH=EF2,只需用t的代数式表示出EF即可解决问题;当
时,S=S正方形EFGH=EF2,只需用t的代数式表示出EF即可解决问题;当![]() <t≤3时,S=S五边形EFGMN=S正方形EFGH-S△MHN=EF2-
<t≤3时,S=S五边形EFGMN=S正方形EFGH-S△MHN=EF2-![]() HNHM,只需用t的代数式分别表示出EF、HN、HM即可解决问题.
HNHM,只需用t的代数式分别表示出EF、HN、HM即可解决问题.
试题解析:(1)当t=1时,PE=2×1=2,PF=1×1=1,EF=EP+PF=2+1=3.
当t=4时,PE=12-2×4=4,PF=1×4=4,EF=EP+PF=4+4=8.
(2)当点H在线段AC上时,
则有AE=HE=EF,即6-2t=3t,
解得:t=![]() .
.
①当0<t≤![]() 时,
时,
EF=EP+PF=2t+t=3t,
则S=9t2;
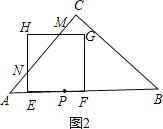
②当![]() <t≤3时,
<t≤3时,
∵∠C=90°,AC=BC,
∴∠A=45°.
∵四边形EFGH是正方形,
∴HE=EF=3t,∠H=∠HEF=90°,
∴∠ANE=90°-45°=45°,
∴∠ANE=∠A=45°,
∴NE=AE=AP-EP=6-2t,
∴HN=HE-NE=3t-(6-2t)=5t-6.
∵∠HNM=∠ANE=45°,
∴∠HMN=90°-45°=45°,
∴∠HMN=∠HNM=45°,
∴HM=HN=5t-6,
∴S=S正方形EFGH-S△NHM
=(3t)2-![]() (5t-6)2
(5t-6)2
=-![]() t2+30t-18.
t2+30t-18.
综上所述:S与t的函数关系式为
S=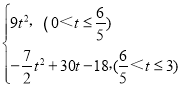 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“任意买一张电影票,座位号是奇数”,此事件是( )
A. 不可能事件 B. 不确定事件 C. 必然事件 D. 确定事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:若3x2﹣2x+b﹣(﹣x﹣bx+1)中不存在含x的一次项,求b值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037 mg,已知1 g=1 000 mg,那么0.000 037 mg用科学记数法表示为( )
A. 3.7×10-5 g B. 3.7×10-6 g C. 3.7×10-7 g D. 3.7×10-8 g
-
科目: 来源: 题型:
查看答案和解析>>【题目】模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.
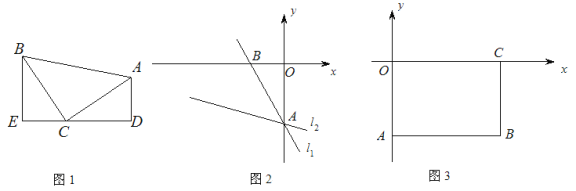
(1)求证:△BEC≌△CDA;
(2)模型应用:
①已知直线l1:y=-
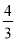 x-4与y轴交于A点,将直线l1绕着A点逆时针旋转45°至l2,如图2,求l2的函数解析式;
x-4与y轴交于A点,将直线l1绕着A点逆时针旋转45°至l2,如图2,求l2的函数解析式;②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,-6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第四象限,且是直线y=-2x+6上的一点,若△APD是不以点A为直角顶点的等腰Rt△,请求出点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,求AB、BC.
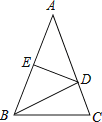
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:

(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
相关试题

