【题目】推理填空:
如图,∠1+∠2=180°,∠A=∠C,试说明:AE∥BC.
解:因为∠1+∠2=180°,
所以AB∥ (同旁内角互补,两直线平行)
所以∠A=∠EDC( ),
又因为∠A=∠C(已知)
所以∠EDC=∠C(等量代换),
所以AE∥BC( )

参考答案:
【答案】见解析.
【解析】
依据平行线的判定,即可得到AB∥DC,进而得出∠EDC=∠C,再根据平行线的判定,即可得到AE∥BC.
因为∠1+∠2=180°,
所以AB∥DC(同旁内角互补,两直线平行)
所以∠A=∠EDC(两直线平行,同位角相等),
又因为∠A=∠C(已知)
所以∠EDC=∠C(等量代换),
所以AE∥BC(内错角相等,两直线平行)
故答案为:DC,两直线平行,同位角相等;内错角相等,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=
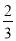 x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣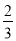 )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )
A. 大于0 B. 等于0 C. 小于0 D. 不能确定
-
科目: 来源: 题型:
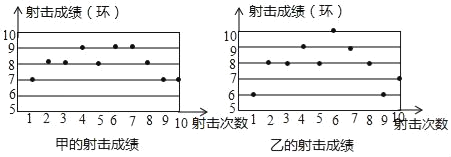
查看答案和解析>>【题目】如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况,则射击成绩的方差较小的是_____(填“甲”或“乙”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学决定到超市购买一定数量的羽毛球拍和羽毛球,已知买1副羽毛球拍和1个羽毛球要花费35元,买2副羽毛球拍和3个羽毛球要花费75元,求购买10副羽毛球拍和20个羽毛球共需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a∥b,直线AB与a,b分别相交于点A,B,AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=3,AB=4,BC=5,求a与b的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN∥OP,点A为直线MN上一定点,B为直线OP上的动点,在直线MN与OP之间且在线段AB的右方作点D,使得AD⊥BD.设∠DAB=α(α为锐角).
(1)求∠NAD与∠PBD的和;(提示过点D作EF∥MN)
(2)当点B在直线OP上运动时,试说明∠OBD﹣∠NAD=90°;
(3)当点B在直线OP上运动的过程中,若AD平分∠NAB,AB也恰好平分∠OBD,请求出此时α的值

相关试题

