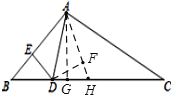
【题目】如图,点D在边BC上,∠C+∠BAD=∠DAC,过D作DE⊥AB于E,![]() ,则线段AC的长为_____.
,则线段AC的长为_____.

参考答案:
【答案】![]()
【解析】
如图,作∠DAH=∠DAE,交BC于H,过点D作DF⊥AH于F,过点A作AG⊥BC于G,根据角平分线的性质可得DE=DF,AE=AF,由∠C+∠BAD=∠DAC可得∠HAC=∠C,即可证明AH=CH,设DE=4x,根据![]() ,利用勾股定理可求出DF、AF的长,设FH=y,在Rt△DFH中,利用勾股定理列方程可求出y值,即可求出DH的长,利用面积法可求出AG的长,利用勾股定理可求出DG的长,即可求出CG的长,利用勾股定理求出AC的长即可得答案.
,利用勾股定理可求出DF、AF的长,设FH=y,在Rt△DFH中,利用勾股定理列方程可求出y值,即可求出DH的长,利用面积法可求出AG的长,利用勾股定理可求出DG的长,即可求出CG的长,利用勾股定理求出AC的长即可得答案.
如图,作∠DAH=∠DAE,交BC于H,过点D作DF⊥AH于F,过点A作AG⊥BC于G,
∵DE⊥AB,
∴DE=DH,AE=AF,
设DE=4x,
∵![]() ,
,
∴AE=7x,
∵AD=![]() ,AE2+AE2=AD2,
,AE2+AE2=AD2,
∴(4x)2+(7x)2=65,
解得:x=1,(负值舍去)
∴DE=4,AE=7,
∴DF=DE=4,DF=AE=7,
∵∠C+∠BAD=∠DAC,∠DAC=∠DAH+∠HAC,
∴∠HAC=∠C,
∴AH=CH,
设FH=y,
∴CH=AH=AF+FH=7+y,
∵CD=13,
∴DH=CD-CH=6-y,
在Rt△DFH中,DF2+FH2=DH2,即42+y2=(6-y)2,
解得:y=![]() ,
,
∴DH=6-![]() =
=![]() ,CH=AH=7+
,CH=AH=7+![]() =
=![]() ,
,
∴S△ADH=![]() DH·AG=
DH·AG=![]() AH·DF,即
AH·DF,即![]() ·AG=
·AG=![]() ×4,
×4,
解得:AG=8,
∴DG=![]() =1,
=1,
∴CG=CD-DG=12,
∴AC=![]() =
=![]() .
.
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等腰直角△ABC沿BC方向平移得到△A'B'C',若
 ,则BB'=________.
,则BB'=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
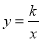 与
与 (
(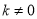 )在同一直角坐标系中的大致图象可能是( )
)在同一直角坐标系中的大致图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2019OB2019,则点A2019的坐标为_______ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘 AB、CD 是否平行;
(2)若 AB∥CD,连接 BC,过点 A 作 AM⊥BC 于 M,垂足为 M,画出图形,并写出∠BCD 与∠BAM 的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2是关于x的一元二次方程
 的两实数根.
的两实数根.(1)求m的范围;
(2)若
 ,求m的值;
,求m的值;(3)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:善于思考的小明在解方程组
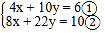 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:
 请你解决以下问题:
请你解决以下问题:(1)试用小明的“整体代换”的方法解方程组

(2)已知 x、y、z,满足
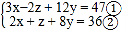 试求 z 的值.
试求 z 的值.
相关试题

