搜索
【题目】如图，将等腰直角△ABC沿BC方向平移得到△A'B'C'，若
，则BB'=________．
参考答案：
【答案】
【解析】
如图，过点P作PD⊥B′C，根据△ABC是等腰直角三角形及平移的性质可得△PB′C是等腰直角三角形，可得PD=B′D=CD，根据△PB′C的面积可求出B′C的长，根据BB′=BC－B′C即可得答案．
如图，过点P作PD⊥B′C，
∵△ABC是等腰直角三角形，
∴∠B=∠ACB=45°，
∵将等腰直角△ABC沿BC方向平移得到△A'B'C'，
∴∠A′B′C=∠B=45°，
∴△PB′C是等腰直角三角形，
∵PD⊥B′C，
∴PD= B′D=CD=
B′C，
∵
，
∴×B′C×PD=×B′C××B′C=4.5，
解得：B′C=
，（负值舍去）
∴BB′=BC-B′C=
=，
故答案为：
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以点A为中心，把△ABC逆时针旋转120°，得到△AB'C′（点B、C的对应点分别为点B′、C′），连接BB'，若AC'∥BB'，则∠CAB'的度数为（ ）
A.45°B.60°C.70°D.90°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF=90°，且EF交正方形的外角∠DCM的平分线CF于点F．
（1）图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE=EF，请叙述你的一个构造方案，并指出是哪两个三角形全等（不要求证明）；
（2）如图2，若点E在线段BC上滑动（不与点B，C重合）．
①AE=EF是否一定成立？说出你的理由；
②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点，当点E滑动到某处时，点F恰好落在此抛物线上，求此时点F的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是用大小相等的小正方形按一定规律拼成的，则第10个图形是_________个小正方形，第n 个图形是___________个小正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】函数
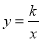与
（
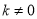）在同一直角坐标系中的大致图象可能是（ ）A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O=2A1O…，依此规律，得到等腰直角三角形A2019OB2019，则点A2019的坐标为_______ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D在边BC上，∠C+∠BAD＝∠DAC，过D作DE⊥AB于E，
，则线段AC的长为_____．
相关试题
