【题目】如图:在数轴上点A表示数a,点B表示数b,点C表示数c,a是多项式2x24x+1的一次项系数,b是最小的正整数,单项式![]() x2y4的次数为c.
x2y4的次数为c.
![]()
(1)a=___,b=___,c=___;
(2)若将数轴在点B处折叠,则点A与点C___重合(填“能”或“不能”);
(3)点A,B,C开始在数轴上运动,若点C以每秒1个单位长度的速度向右运动,同时,点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功,t分钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB=___,BC=___(用含t的代数式表示);
(4)请问:3ABBC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
参考答案:
【答案】(1)-4, 1, 6;(2)能;(3)t+5,3t+5;(4)10
【解析】
(1)根据多项式与单项式的概念即可求出答案.
(2)只需要判断A、C是否关于B对称即可.
(3)根据A、B、C三点运动的方向即可求出答案.
(4)将(3)问中的AB与BC的表达式代入即可判断.
(1)∵多项式2x24x+1的一次项系数是-4,最小的正整数是1,单项式![]() x2y4的次数为6,
x2y4的次数为6,
∴a=-4,b=1,c=6;
(2)能重合,由于-4与6的中点为1,故将数轴在点B处折叠,则点A与点C能重合;
(3)由于点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运动,
∴t秒钟后,AB=3t+1-(-4)-2t=t+5;
由于点C以每秒1个单位长度的速度向右运动,
∴t秒钟后,BC=2t+6-1+t=3t+5;
(4)3AB-BC=3(t+5)-3t-5=3t+15-3t-5=10,
∴3AB-BC的值不会随着时间t的变化而改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
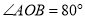 ,
,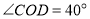 ,
,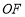 为
为 的角平分线.
的角平分线.(1)如图1,若
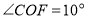 ,则
,则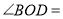 ______;若
______;若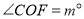 ,则
,则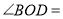 ______;猜想:
______;猜想: 与
与 的数量关系为______
的数量关系为______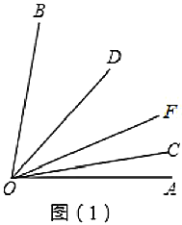
(2)当
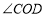 绕点
绕点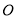 按逆时针旋转至图2的位置时,(1)的数量关系是否仍然成立?请说明理由.
按逆时针旋转至图2的位置时,(1)的数量关系是否仍然成立?请说明理由.
(3)如图3,在(2)的条件下,在
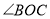 中作射线
中作射线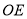 ,使
,使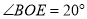 ,且
,且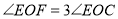 ,直接写出
,直接写出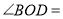 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=
 .
.①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有三个分别标有数字1,2,4的小球,它们的形状、大小、质地等完全相同,小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)写出(x,y)的所有可能出现的结果;
(2)小明、小华各取一次,由取出小球所确定的数字作为点的坐标,这样的点(x,y)中落在反比例函数y=
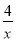 的图象上的点的概率是多少?
的图象上的点的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(
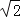 ≈1.414,精确到1米)
≈1.414,精确到1米)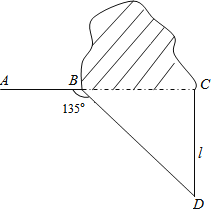
-
科目: 来源: 题型:
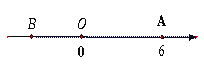
查看答案和解析>>【题目】如图,已知数轴上的点A对应的数为6,B是数轴上的一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿着数轴向左匀速运动,设运动时间为t秒(t>0).
(1)数轴上点B对应的数是_______,点P对应的数是_______(用t的式子表示);
(2)动点Q从点B与点P同时出发,以每秒4个单位长度的速度沿着数轴向左匀速运动,试问:运动多少时间点P可以追上点Q?
(3)M是AP的中点,N是PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若有变化,说明理由;若没有变化,请你画出图形,并求出MN的长.
相关试题

