【题目】![]() ,
,![]() ,
,![]() 为
为![]() 的角平分线.
的角平分线.
(1)如图1,若![]() ,则
,则![]() ______;若
______;若![]() ,则
,则![]() ______;猜想:
______;猜想:![]() 与
与![]() 的数量关系为______
的数量关系为______
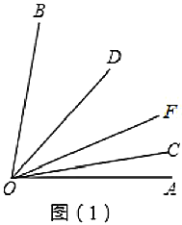
(2)当![]() 绕点
绕点![]() 按逆时针旋转至图2的位置时,(1)的数量关系是否仍然成立?请说明理由.
按逆时针旋转至图2的位置时,(1)的数量关系是否仍然成立?请说明理由.
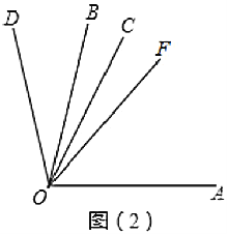
(3)如图3,在(2)的条件下,在![]() 中作射线
中作射线![]() ,使
,使![]() ,且
,且![]() ,直接写出
,直接写出![]() ______.
______.

参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)见解析;(3)16°
;(2)见解析;(3)16°
【解析】
(1)由已知求出∠DOF=30°,由角平分线得出∠AOF=∠DOF=30°,得出∠AOD=60°,求出∠BOD=∠AOB-∠AOD=20°;若∠COF=m°,则∠DOF=40°-m°,由角平分线得出∠AOF=∠DOF=40°-m°,得出∠AOD=80°-2m°,得出∠BOD=∠AOB-∠AOD=2m°,即可得出结论;
(2)设![]() ,则
,则![]() ,利用角平分线的性质即可得出
,利用角平分线的性质即可得出![]() ,(1)的数量关系依然成立;
,(1)的数量关系依然成立;
(3)设![]() ,则
,则![]() ,得出
,得出![]() ,由角平分线得出
,由角平分线得出![]() ,由∠AOB=80°得出方程,解方程求出
,由∠AOB=80°得出方程,解方程求出![]() ,即可得出结果.
,即可得出结果.
(1)∵![]() ,
,![]()
∴∠FOD=∠COD-∠COF=40°-10°=30°
∵![]() 为
为![]() 的角平分线
的角平分线
∴∠AOD=2∠FOD=60°
∵![]() ,
,
∴∠BOD=∠AOB-∠AOD=80°-60°=20°
同理可得,∠BOD=![]() ,
,
∵∠COD=40°,∠COF=10°,
∴∠DOF=30°,
∵OF为∠AOD的角平分线.
∴∠AOF=∠DOF=30°,
∴∠AOD=60°,
∴∠BOD=∠AOB-∠AOD=20°;
∵∠COD=40°,∠COF=m°,
∴∠DOF=40°-m°,
∵OF为∠AOD的角平分线.
∴∠AOF=∠DOF=40°-m°,
∴∠AOD=80°-2m°,
∴∠BOD=∠AOB-∠AOD=2m°,
∴∠BOD=2∠COF;
通过上述两种求法,可得![]() .
.
(2)∵![]() ,设
,设![]() ,则
,则![]() .
.
∵![]() 为
为![]() 的角平分线,
的角平分线,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() .(1)的数量关系依然成立.
.(1)的数量关系依然成立.
(3)设![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的平分线,
的平分线,
∴![]()
∵![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]()
-
科目: 来源: 题型:
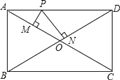
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )
A.
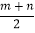 B.
B.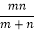 C.
C.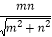 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=
 (x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.
(x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,点A(﹣2,2)和点B(﹣3,﹣2)的位置如图所示.
(1)作出线段AB关于y轴对称的线段A′B′,并写出点A、B的对称点A′、B′的坐标;
(2)连接AA′和BB′,请在图中画一条线段,将图中的四边形AA′B′B分成两个图形,其中一个是轴对称图形,另一个是中心对称图形,并且线段的一个端点为四边形的顶点,另一个端点在四边形一边的格点上.(每个小正方形的顶点均为格点).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=
 .
.①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上点A表示数a,点B表示数b,点C表示数c,a是多项式2x24x+1的一次项系数,b是最小的正整数,单项式
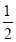 x2y4的次数为c.
x2y4的次数为c.
(1)a=___,b=___,c=___;
(2)若将数轴在点B处折叠,则点A与点C___重合(填“能”或“不能”);
(3)点A,B,C开始在数轴上运动,若点C以每秒1个单位长度的速度向右运动,同时,点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功,t分钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB=___,BC=___(用含t的代数式表示);
(4)请问:3ABBC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
相关试题

