【题目】“足球运球”是中考体育必考项目之一兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.
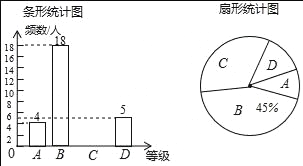
根据所给信息,解答以下问题
(1)本次一共抽取了 名九年级学生;
(2)补全条形统计图;
(3)在扇形统计图中,C对应的扇形的圆心角是 度;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
参考答案:
【答案】(1)40;(2)补图见解析;(3)117;(4)30人
【解析】
(1)先根据B等级人数及其百分比求得总人数;
(2)求出C组人数即可补全图形;
(3)总人数减去其他等级人数求得C等级人数,继而用360°乘以C等级人数所占比例即可得;
(4)总人数乘以样本中A等级人数所占比例可得.
解:(1)总人数为18÷45%=40人,
故答案为40.
(2)C等级人数为40﹣(4+18+5)=13人,
补全条形图如下:

(3)则C对应的扇形的圆心角是360°×![]() =117°,
=117°,
故答案为:117;
(4)估计足球运球测试成绩达到A级的学生有300×![]() =30人.
=30人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片 ABCD 折叠,AE、EF 为折痕,点 C 落在 AD 边上的 G 处, 并且点 B 落在 EG 边的 H 处,若 AB=
 ,∠BAE=30°,则 BC 边的长为( )
,∠BAE=30°,则 BC 边的长为( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
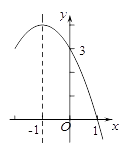
A.x=1
B.x=﹣1
C.x1=1,x2=﹣3
D.x1=1,x2=﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程
 =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程
 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=60cm,在直线AB上画线段BC,使BC=20cm,点D是AC的中点,求CD的长度.
相关试题

