【题目】如图,在![]() 中,
中,![]() 是角平分线,
是角平分线,![]() ,
,
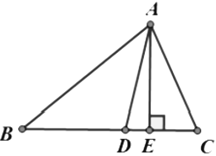
(1)求![]() 的度数.
的度数.
(2)过点![]() 作
作![]() 边上的高
边上的高![]() , 垂足为
, 垂足为![]() ;求
;求![]() 的度数.
的度数.
参考答案:
【答案】(1)∠BAD=35°;(2)∠EAD=15°.
【解析】
(1)根据三角形内角和定理求出∠BAC的度数,根据角平分线得定义即可求出∠BAD的度数;
(2)由直角三角形两锐角互余的关系可求出∠CAE的度数,根据角平分线的定义可求出∠CAD的度数,根据角的和差关系即可求出∠EAD的度数.
(1)∵∠B=40°,∠C=70°,∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=70°,
∵![]() 是角平分线,
是角平分线,
∴∠BAD=∠CAD=![]() ∠BAC=35°.
∠BAC=35°.
(2)∵AE为BC边上的高,
∴∠AEC=90°,
∵∠C=70°,
∴∠CAE=90°-∠C=20°,
∵∠CAD=35°,
∴∠EAD=∠CAD-∠CAE=15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①
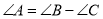 ,②
,② ,③
,③ ,④
,④ 中,能确定
中,能确定 是直角三角形的条件有( )
是直角三角形的条件有( )A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):

(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
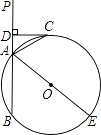
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
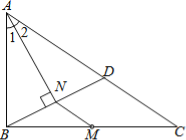
(1)求证:BN=DN;
(2)求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机械厂甲、乙两个生产车间承担生产同一种零件的任务,甲、乙两车间共有
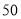 人,甲车间平均每人每天生产零件
人,甲车间平均每人每天生产零件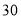 个.乙车间平均每人每天生产零件
个.乙车间平均每人每天生产零件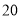 个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为
个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为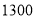 个.
个.(1)求甲、乙两车间各有多少人?
(2)该机械厂改进了生产技术.在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间.调整后甲车间平均每人每天生产零件
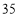 个,乙车间平均每人每天生产零件
个,乙车间平均每人每天生产零件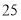 个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于
个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于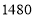 个,求从甲车间最多调出多少人到乙车间.
个,求从甲车间最多调出多少人到乙车间.
相关试题

