【题目】如图,公共汽车行驶在笔直的公路上,这条路上有![]() 四个站点,每相邻两站之间的距离为
四个站点,每相邻两站之间的距离为![]() 千米,从
千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔
站同时发车,相向而行,且以后上行车、下行车每隔![]() 分钟分别在
分钟分别在![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为![]() 千米/小时.
千米/小时.
![]() 第一班上行车到
第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
![]() 第一班上行车与第一班下行车发车后多少小时相距
第一班上行车与第一班下行车发车后多少小时相距![]() 千米?
千米?
![]() 一乘客在
一乘客在![]() 两站之间的
两站之间的![]() 处,刚好遇到上行车,
处,刚好遇到上行车,![]() 千米,他从
千米,他从![]() 处以
处以![]() 千米/小时的速度步行到
千米/小时的速度步行到![]() 站乘下行车前往
站乘下行车前往![]() 站办事.
站办事.

①若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
②若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
参考答案:
【答案】(1)第一班上行车到![]() 站用时
站用时![]() 小时,第一班下行车到
小时,第一班下行车到![]() 站用时
站用时![]() 小时;(2)第一班上行车与第一班下行车发车后
小时;(2)第一班上行车与第一班下行车发车后![]() 小时或
小时或![]() 小时相距
小时相距![]() 千米;(3)①
千米;(3)①![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要
站的时间最少要![]() 分钟;②
分钟;②![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要
站的时间最少要![]() 分钟.
分钟.
【解析】
(1)根据时间=路程÷速度计算即可;
(2)设第一班上行车与第一班下行车发车t小时相距![]() 千米,然后根据相遇前和相遇后分类讨论,分别列出对应个方程即可求出t;
千米,然后根据相遇前和相遇后分类讨论,分别列出对应个方程即可求出t;
(3)由题意知:同时出发的一对上、下行车的位置关于![]() 中点对称,乘客右侧第一辆下行车离
中点对称,乘客右侧第一辆下行车离![]() 站也是
站也是![]() 千米,这辆下行车离
千米,这辆下行车离![]() 站是
站是![]() 千米
千米
①先求出点P到点B的时间和乘客右侧第一辆下行车到达![]() 站的时间,比较即可判断乘客能否乘上右侧第一辆下行车,从而求出乘客从
站的时间,比较即可判断乘客能否乘上右侧第一辆下行车,从而求出乘客从![]() 处到达
处到达![]() 站的最少时间;
站的最少时间;
②先求出点P到点B的时间和乘客右侧第一辆下行车到达![]() 站的时间,比较即可判断乘客能否乘上右侧第一辆下行车,如不能乘上第一辆车,还需算出能否乘上右侧第二辆下行车,从而求出乘客从
站的时间,比较即可判断乘客能否乘上右侧第一辆下行车,如不能乘上第一辆车,还需算出能否乘上右侧第二辆下行车,从而求出乘客从![]() 处到达
处到达![]() 站的最少时间.
站的最少时间.
解:![]() 第一班上行车到
第一班上行车到![]() 站用时
站用时![]() 小时,
小时,
第一班下行车到![]() 站用时
站用时![]() 小时;
小时;
![]() 设第一班上行车与第一班下行车发车t小时相距
设第一班上行车与第一班下行车发车t小时相距![]() 千米.
千米.
①相遇前:
![]() .
.
解得![]()
②相遇后:
![]()
解得![]()
答:第一班上行车与第一班下行车发车后![]() 小时或
小时或![]() 小时相距
小时相距![]() 千米;
千米;
(3)由题意知:同时出发的一对上、下行车的位置关于![]() 中点对称,乘客右侧第一辆下行车离
中点对称,乘客右侧第一辆下行车离![]() 站也是
站也是![]() 千米,这辆下行车离
千米,这辆下行车离![]() 站是
站是![]() 千米.
千米.
①若![]() 千米,
千米,
乘客从![]() 处走到
处走到![]() 站的时间
站的时间![]() (小时),
(小时),
乘客右侧第一辆下行车到达![]() 站的时间
站的时间![]() (小时),
(小时),
![]()
![]() 乘客能乘上右侧第一辆下行车.
乘客能乘上右侧第一辆下行车.
![]() (分钟)
(分钟)
答:若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要
站的时间最少要![]() 分钟.
分钟.
②若![]() 千米,
千米,
乘客从![]() 处走到
处走到![]() 站的时间
站的时间![]() (小时),
(小时),
乘客右侧第一辆下行车到达![]() 站的时间
站的时间![]() (小时),
(小时),
![]()
![]() 乘客不能乘上右侧第一辆下行车,
乘客不能乘上右侧第一辆下行车,
![]()
![]() 乘客能乘上右侧第二辆下行车.
乘客能乘上右侧第二辆下行车.
![]() (分钟)
(分钟)
答:若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要
站的时间最少要![]() 分钟.
分钟.
-
科目: 来源: 题型:
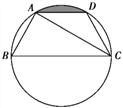
查看答案和解析>>【题目】如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且
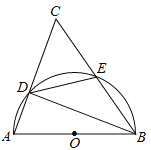
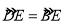 .
.
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求
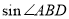 的值.
的值. -
科目: 来源: 题型:
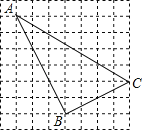
查看答案和解析>>【题目】已知图中的每个方格都是边长为1的小正方形,每个小正方形的顶点称为格点,△ABC的顶点在格点上,称为格点三角形,请按要求完成下列各题
(1)填空:
AB= ,BC= ,AC= ;
(2)试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运城市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:
A.绿化造林 B.汽车限行 C.拆除燃煤小锅炉 D.使用清洁能源.
调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整.
(3)求图2中
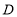 项目对应的扇形的圆心角的度数.
项目对应的扇形的圆心角的度数.(4)请你结合自己的实际情况对有效治理雾霾提几点建议.(至少写一条)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:
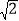 ≈1.41,
≈1.41,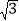 ≈1.73)
≈1.73)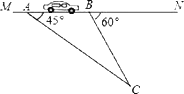
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线y=
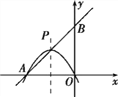
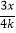 +3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-
+3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=- x2+bx+c经过点A,P,O(原点).
x2+bx+c经过点A,P,O(原点).(1)求抛物线的表达式;
(2)在x轴上方的抛物线上是否存在一点Q,使∠QAO=45°?如果存在,求出Q点的坐标;如果不存在,请说明理由.
相关试题

