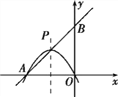
【题目】如图所示,直线y=![]() +3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-
+3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-![]() x2+bx+c经过点A,P,O(原点).
x2+bx+c经过点A,P,O(原点).
(1)求抛物线的表达式;
(2)在x轴上方的抛物线上是否存在一点Q,使∠QAO=45°?如果存在,求出Q点的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)抛物线的表达式为y=-![]() x2-
x2-![]() x;(2)存在,Q点的坐标为
x;(2)存在,Q点的坐标为![]() .
.
【解析】(1)根据直线AB的解析式,可求得B点坐标,而P为线段AB的中点,那么点P的纵坐标为B点纵坐标的一半,由于抛物线经过原点,那么c=0,根据公式法表示出P点纵坐标,即可求得b的值,由此确定该抛物线的解析式.(2)此题应分两种情况讨论:①当Q点在x轴上方时,由于∠OAQ=45°,那么直线AQ的斜率为k=1,而A点坐标易求得,即可得到直线AQ的解析式,联立抛物线的解析式,即可求得Q点坐标;
②当Q点在x轴下方时,方法同①.
(1)直线y=![]() +3与x轴、y轴分别交于点A,B,且P为线段AB的中点,抛物线y=-
+3与x轴、y轴分别交于点A,B,且P为线段AB的中点,抛物线y=-![]() x2+bx+c过A,P,O三点,
x2+bx+c过A,P,O三点,
∴OB=3,c=0,P必为抛物线的顶点,
∴![]() =
=![]() ,∴b=±
,∴b=±![]() .
.
又∵x=-![]() =
=![]() <0,∴b<0,∴b=-
<0,∴b<0,∴b=-![]() .
.
∴抛物线的表达式为y=-![]() x2-
x2-![]() x.
x.
(2)存在.
∵抛物线y=-![]() x2-
x2-![]() x经过点A,
x经过点A,
∴A点的坐标为(-4,0).
设Q点的坐标为(x,y),∵∠QAO=45°,
∴x=-4+y.
将其代入抛物线的关系式中得y=-![]() (-4+y)2-
(-4+y)2-![]() (-4+y),解得y1=0(舍去),y2=
(-4+y),解得y1=0(舍去),y2=![]() .
.
当y=![]() 时,x=-
时,x=-![]() .
.
∴Q点的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,公共汽车行驶在笔直的公路上,这条路上有
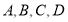 四个站点,每相邻两站之间的距离为
四个站点,每相邻两站之间的距离为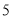 千米,从
千米,从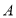 站开往
站开往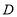 站的车称为上行车,从
站的车称为上行车,从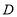 站开往
站开往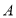 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从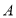 站、
站、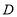 站同时发车,相向而行,且以后上行车、下行车每隔
站同时发车,相向而行,且以后上行车、下行车每隔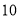 分钟分别在
分钟分别在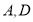 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为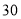 千米/小时.
千米/小时.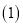 第一班上行车到
第一班上行车到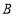 站、第一班下行车到
站、第一班下行车到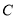 站分别用时多少?
站分别用时多少?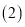 第一班上行车与第一班下行车发车后多少小时相距
第一班上行车与第一班下行车发车后多少小时相距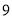 千米?
千米?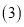 一乘客在
一乘客在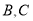 两站之间的
两站之间的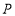 处,刚好遇到上行车,
处,刚好遇到上行车,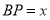 千米,他从
千米,他从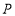 处以
处以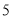 千米/小时的速度步行到
千米/小时的速度步行到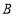 站乘下行车前往
站乘下行车前往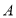 站办事.
站办事.
①若
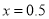 千米,乘客从
千米,乘客从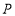 处到达
处到达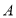 站的时间最少要几分钟?
站的时间最少要几分钟?②若
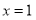 千米,乘客从
千米,乘客从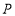 处到达
处到达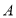 站的时间最少要几分钟?
站的时间最少要几分钟? -
科目: 来源: 题型:
查看答案和解析>>【题目】运城市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:
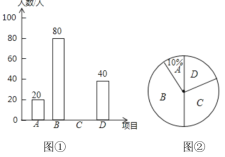
A.绿化造林 B.汽车限行 C.拆除燃煤小锅炉 D.使用清洁能源.
调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整.
(3)求图2中
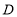 项目对应的扇形的圆心角的度数.
项目对应的扇形的圆心角的度数.(4)请你结合自己的实际情况对有效治理雾霾提几点建议.(至少写一条)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:
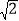 ≈1.41,
≈1.41,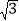 ≈1.73)
≈1.73)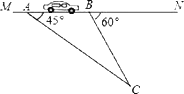
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发市场规定,一次购买苹果不超过100kg(包括100kg),批发价为5元,如果一次购买100kg以上苹果,超过100kg的部分苹果价格打8折.
(I)请填写下表
购买量/kg
0
50
100
150
200
…
付款金额/元
0
250
_
700
__
…
(Ⅱ)写出付款金额关于购买量的函数解析式;
(Ⅲ)如果某人付款2100元,求其购买苹果的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)求证:四边形AECF是菱形;
(2)若AC=4,BE=1,直接写出菱形AECF的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】云南鲁甸6.5级地震后,空军某部奉命赴灾区空投救灾物资,已知物资离开飞机在空中沿抛物线降落,抛物线的顶点在机舱舱口点A处(如图所示).
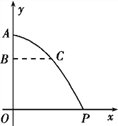
(1)若物体离开A处后下落的竖直高度AB=160 m时,水平距离BC=200 m,那么要使飞机在竖直高度OA=1 km的空中空投的物资恰好落在居民点P处,求飞机到点P处的水平距离OP应为多少;
(2)根据当时的风力测算,空投物资离开A处的竖直距离为160 m时,它到A处的水平距离将增至400 m.要使飞机在(1)中的点O正上方空投物资到P处,飞机离地面的高度应为多少?
相关试题

