【题目】如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数. 下面提供三种思路:
(1)过点F作FH∥AB;
(2)延长EF交CD于M;
(3)延长GF交AB于K. 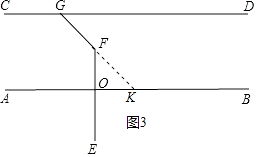
请你利用三个思路中的两个思路,将图形补充完整,求∠EFG的度数.
解(一):
解(二):
参考答案:
【答案】
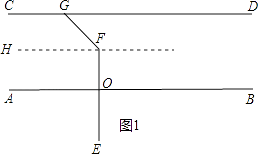
(1)
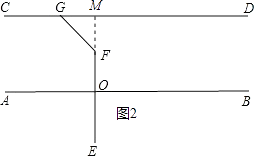
(2)
(3)解(一):利用思路(1)过点F 作FH∥AB,如图1所示.

∵EF⊥AB,
∴∠BOF=90°.
∵FH∥AB,AB∥CD,
∴FH∥CD.
∵∠FGC+∠GFH=180°,∠FGC=131°,
∴∠GFH=49°,
∴∠GFO=∠GFH+∠HFO=49°+90°=139°.
解(二):利用思路(2)延长EF交CD于M,如图2所示.

∵EF⊥AB,
∴∠BOF=90°.
∵AB∥CD,
∴∠GMF=∠BOF=90°.
∵∠FGC=131°,
∴∠FGM=49°.
∵∠FGM+∠GMF+∠MFG=180°,
∴49°+90°+∠MFG=180°,
∴∠MFG=41°,
∴∠GFO=180°﹣∠MFG=139°.
解(三):利用思路(3)延长GF交AB于K,如图3所示.
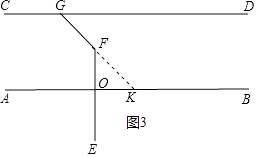
∵EF⊥AB,
∴∠KOF=90°.
∵CD∥AB,
∴∠FKO+∠FGC=180°.
∵∠FGC=131°,
∴∠FKO=49°.
∵∠FKO+∠KOF+∠OFK=180°,
∴49°+90°+∠OFK=180°,
∴∠OFK=41°,
∴∠GFO=180°﹣∠OFK=139°.
【解析】(1)由EF⊥AB可得出∠BOF=90°,根据“平行于同一条直线的两直线互相平行”可得出FH∥CD,由“两直线平行,同旁内角互补”可得出∠GFH=49°,进而即可求出∠EFG的度数;(2)由EF⊥AB可得出∠BOF=90°,由“两直线平行,内错角相等”可得出∠GMF=∠BOF=90°,利用邻补角互补可求出∠FGM=49°,再根据三角形内角和定理可求出∠MFG=41°,结合邻补角互补可求出∠EFG的度数;(3)由EF⊥AB可得出∠KOF=90°,由“两直线平行,同旁内角互补”可得出∠FKO=49°,利用三角形内角和定理可得出∠OFK=41°,再利用邻补角互补可求出∠EFG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空: 完成下列证明:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.
试说明:AC∥DF
解:∵∠1=∠2,(已知)
∠1=∠3()
∴∠2=∠3,(等量代换)
∴∥ , ()
∴∠C=∠ABD,()
又∵∠C=∠D,(已知)
∴∠D=∠ABD,()
∴AC∥DF.()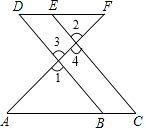
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线CD与直线AB相交于点C,根据下列语句画图(注:可利用三角尺画图,但要保持图形清晰)
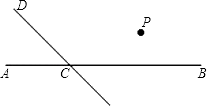
(1)过点P作PQ∥AB,交CD于点Q,过点P作PR⊥CD,垂足为R;
(2)若∠DCB=120°,则∠QRC是多少度?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若线段AB平行于x轴,AB的长为4,且A的坐标为(2,3),求点B的坐标.
-
科目: 来源: 题型:
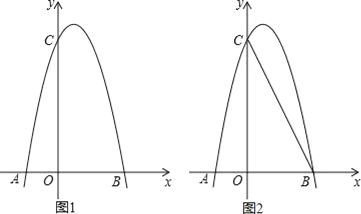
查看答案和解析>>【题目】如图1,对称轴为直线x=
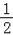 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“生态兴化,如诗如画”.我市正全力打造成国家全域旅游示范区,为调查我市市民对兴化全域旅游的情况了解,宜采用_________(填“普查”或“抽样调查”)的方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解一批空调的寿命,从中抽取100台空调进行试验,这个问题中的样本是( )
A. 这批空调的寿命 B. 抽取的100台空调
C. 100 D. 抽取的100台空调的寿命
相关试题

