搜索
【题目】已知x=1是一元二次方程x2﹣mx+2=0的一个根，则m= ．
参考答案：
【答案】3
【解析】解：依题意得：12﹣m×1+2=0， 解得m=3．
故答案是：3．
把x=1代入已知方程得到关于m的一元一次方程，通过解该方程求得m的值即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】操作探究：已知在纸面上有一数轴（如图所示），
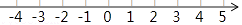
（1）操作一： 折叠纸面，使数字1表示的点与﹣1表示的点重合，则﹣3表示的点与表示的点重合；
（2）操作二： 折叠纸面，使﹣1表示的点与5表示的点重合，回答以下问题：
①10表示的点与数表示的点重合；
（3）②若数轴上A、B两点之间距离为15，（A在B的左侧），且A、B两点经折叠后重合，求A、B两点表示的数是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b，c是△ABC的三边长，且满足a2＋2ab＝c2＋2bc，试判断这个三角形的形状．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AC平分∠BAD，CD⊥AD，CB⊥AB，连结BD.请找出图中所有的等腰三角形，并说明理由．
-
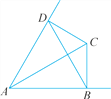
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标中，抛物线y=ax2﹣3ax﹣10a（a＞0）分别交x轴于点A、B（点A在点B左侧），交y轴于点C，且OB=OC．
（1）求a的值；
（2）如图1，点P位抛物线上一动点，设点P的横坐标为t（t＞0），连接AC、PA、PC，△PAC的面积为S，求S与t之间的函数关系式；
（3）如图2，在（2）的条件下，设对称轴l交x轴于点H，过P点作PD⊥l，垂足为D，在抛物线、对称轴上分别取点E、F，连接DE、EF，使PD=DE=EF，连接AE交对称轴于点G，直线y=kx﹣
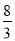k（k≠0）恰好经过点G，将直线y=kx﹣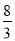k沿过点H的直线折叠得到对称直线m，直线m恰好经过点A，直线m与第四象限的抛物线交于另一点Q，若
=
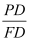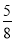，求点Q的坐标．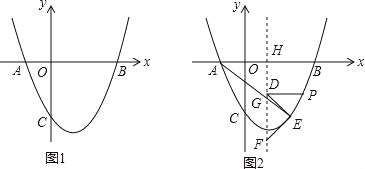
-
科目： 来源： 题型：
查看答案和解析>>【题目】矩形的两条对角线的一个交角为60°，两条对角线的和为8cm，则这个矩形的一条较短边为cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若x2﹣kxy+9y2是一个完全平方式，则k的值为（ ）
A. 3 B. ±6 C. 6 D. +3
相关试题
