搜索
【题目】下列函数中，满足y的值随x的值增大而增大的是（ ）
A.y=﹣2x
B.y=3x﹣1
C.y= 
D.y=x2
参考答案：
【答案】B
【解析】解：A、在y=﹣2x中，k=﹣2＜0，
∴y的值随x的值增大而减小；
B、在y=3x﹣1中，k=3＞0，
∴y的值随x的值增大而增大；
C、在y= 
中，k=1＞0，
∴y的值随x的值增大而减小；
D、二次函数y=x2 ，
当x＜0时，y的值随x的值增大而减小；
当x＞0时，y的值随x的值增大而增大．
故选B．
【考点精析】通过灵活运用一次函数的性质和反比例函数的性质，掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了解全校同学五一假期参加社团活动的情况，抽查了100名同学，统计它们假期参加社团活动的时间，绘成频数分布直方图（如图），则参加社团活动时间的中位数所在的范围是（ ）
A.4﹣6小时
B.6﹣8小时
C.8﹣10小时
D.不能确定 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，双曲线
（x＜0）经过平行四边形ABCO的对角线交点D，已知边OC在y轴上，且AC⊥AB于点C，则平行四边形ABCO的面积是（ ）
A.
B. 
C. 3 D. 6【答案】A
【解析】试题分析：∵点D为平行四边形ABCO的对角线交点，双曲线y＝
（x＜0）经过点D，AC⊥y轴，∴S平行四边形ABCO＝4S△COD＝4×
×|
|＝
．故选A．
点睛：本题考查了反比例函数系数k的几何意义以及平行四边形的性质，根据平行四边形的性质结合反比例函数系数k的几何意义，找出S平行四边形ABCO＝4S△COD＝2|k|是解题的关键．
【题型】单选题
【结束】
9【题目】如果分式
在实数范围内有意义，则
的取值范围是_____________. -
科目： 来源： 题型：
查看答案和解析>>【题目】根据所学知识完成题目：
（1）一个角的余角与补角的和是这个角的补角与余角的差的两倍，求这个角．
（2）从两点三十分时开始算起，钟表上的时针与分针经过多久第一次重合？
-
科目： 来源： 题型：
查看答案和解析>>【题目】用两种正多边形铺满地面，其中一种是正八边形，则另一种正多边形是（ ）。
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目： 来源： 题型：
查看答案和解析>>【题目】当m=________时，函数
是反比例函数.【答案】2
【解析】试题分析：∵函数y＝(m＋2)x|m|－3是反比例函数，
∴m＋2≠0且|m|－3＝－1，
解得m＝2．
故答案为2．
点睛：本题考查了反比例函数的定义：若两个变量x与y满足y＝
（k≠0）的关系式，则y与x称为反比例函数．【题型】填空题
【结束】
12【题目】为弘扬中华传统文化，某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力，从中抽取部分学生的成绩（得分取正整数，满分为100分）进行统计分析，得到分数段在70.5～80.5的频数是50，所占百分比25％，则本次抽样调查的样本容量为_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，AD=2AB=4，E是AD的中点，一块足够大的三角板的直角顶点与点E重合，将三角板绕点E旋转，三角板的两直角边分别交AB，BC（或它们的延长线）于点M，N，设∠AEM=α（0°＜α＜90°），给出下列四个结论：
①AM=CN；
②∠AME=∠BNE；
③BN﹣AM=2；
④S△EMN=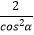
．
上述结论中正确的个数是（ ）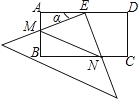
A.1
B.2
C.3
D.4
相关试题
