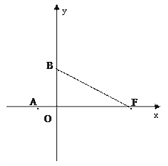
【题目】已知抛物线经过点A(-3, 0),F(8, 0),B(0, 4)三点.
(1)求抛物线解析式及对称轴.
(2)若点D在线段FB上运动(不与F,B重合),过点D作DC⊥轴于点C(x, 0),将△FCD沿CD向左翻折,点B对应点为点E, △CDE与△FBO重叠部分面积为S.
①试求出S与x之间的函数关系式,并写出自变量取值范围.
②是否存在这样的点C,使得△BDE为直角三角形,若存在,求出C点坐标,若不存在,请说明理由;
(3)抛物线对称轴上有一点M,平面内有一点N,若以A,B,M,N四点组成的四边形为菱形,求点N的坐标;

参考答案:
【答案】(1)![]() , 对称轴
, 对称轴![]() ;(2) ①
;(2) ①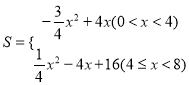 ;②存在,
;②存在, ![]() 或
或![]() ; (3)
; (3) 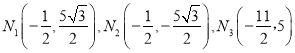 .
.
【解析】试题分析:(1)利用待定系数法即可求出;(2) ①C点的位置应分两种情况进行讨论,当C在OF的中点或在中点与F之间时,重合部分是△CDE;当C在OF的中点与O之间时,重合部分是梯形,就可以得到函数解析式.②分△BDE以点B为直角顶点和△BDE以点E为直角顶点,两种情况进行讨论.根据相似三角形的对应边的比相等,求出OE的长,就可以得到C点的坐标;(3)①AB为边,②AB为对角线,分两种情况分析讨论就能得到答案.
试题解析:
(1)设抛物线解析式为y=a(x+3)(x-8),把(0,4)代入得4=a×3×(-8),解得![]() ,
,
∴![]()
此时,抛物线的对称轴为:直线![]()
(2)①
②当∠BED=90°时,△BOE∽△ECD
∴![]() ,
,![]() ,
,
∴EO=2
∴EC=3
∴![]()
当∠EBD=90°时,△EOB∽△BOF
∴EO=2,
∴EC=(2+8)/2,
∴![]()
(3)①以AB为边,以B为圆心,AB为半径画圆交对称轴于![]() 两点,
两点,
![]() ,
,
由![]() 平移至
平移至![]() 得,
得,
![]() ,
,![]() ,
,
以A为圆心,AB为半径画圆,此时与对称轴没有交点,
故不存在.
②AB为对角线,直线AB的解析式为: ![]() ,
,
则AB的中垂线MN的解析式为: ![]() ,
,
当![]() 时 ,y=-1
时 ,y=-1
∴![]() ,
,![]() .
.
综上所述: ![]() ,
, ![]() ,
, ![]() .
.
点睛:此题综合考查了相似综合题,其中涉及到了待定系数法求二次函数的解析式、二次函数最值的求法,相似三角形的判定与性质以及多边形面积的求法等知识点. 解答此类关于函数的综合性应用题要善于设点,然后利用点与直线的关系或者点与其他函数的关系,然后把题中所有可能用到的点用只含一个未知数的方程表达出来.此题难度较大,注意掌握函数思想、分类讨论思想与树形结合思想的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.

(1)在这次随机抽样调查中,共抽查了多少名学生留守儿童?
(2)扇形统计图中C类所占的圆心角是°;这次调查中为D类的留守儿童有人;
(3)请你估计该县20000名留守儿童中,出现较为严重问题及以上的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
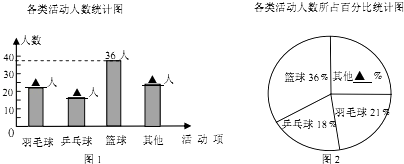
(1)学校采用的调查方式是;学校共选取了名学生;
(2)补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他%;
(3)该校共有1100名学生,请估计喜欢“篮球”的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.随机抛掷一枚硬币,反面一定朝上
B.数据3,3,5,5,8的众数是8
C.某商场抽奖活动获奖的概率为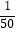 ,说明毎买50张奖券中一定有一张中奖
,说明毎买50张奖券中一定有一张中奖
D.想要了解广安市民对“全面二孩”政策的看法,宜采用抽样调查 -
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的
 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:9xy3﹣xy=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
(1)求∠EOF的度数;
(2)若将条件“∠AOB是直角,∠BOC=60°”改为:∠AOB=x°,∠EOF=y°,其它条件不变.
①则请用x的代数式来表示y;
②如果∠AOB+∠EOF=156°.则∠EOF是多少度?

相关试题

