【题目】抛物线y=![]() x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() .(2)点A/的坐标为(﹣3,4).点A/在该抛物线上.(3)点P运动到
.(2)点A/的坐标为(﹣3,4).点A/在该抛物线上.(3)点P运动到![]() 时,四边形PACM是平行四边形.
时,四边形PACM是平行四边形.
【解析】试题分析:(1)利用待定系数法求出抛物线的解析式;
(2)首先求出对称点A′的坐标,然后代入抛物线解析式,即可判定点A′是否在抛物线上.本问关键在于求出A′的坐标.如答图所示,作辅助线,构造一对相似三角形Rt△A′EA∽Rt△OAC,利用相似关系、对称性质、勾股定理,求出对称点A′的坐标;
(3)本问为存在型问题.解题要点是利用平行四边形的定义,列出代数关系式求解.如答图所示,平行四边形的对边平行且相等,因此PM=AC=10;利用含未知数的代数式表示出PM的长度,然后列方程求解.
试题解析:(1)∵![]() 与x轴交于A(5,0)、B(-1,0)两点,
与x轴交于A(5,0)、B(-1,0)两点,
∴ ,
,
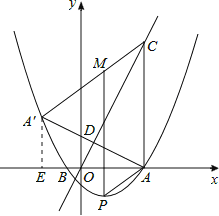
解得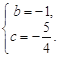
∴抛物线的解析式为![]() .
.
(2) 过点![]() 作
作![]() ⊥x轴于E,AA/与OC交于点D,
⊥x轴于E,AA/与OC交于点D,
∵点C在直线y=2x上,
∴C(5,10)
∵点A和![]() 关于直线y=2x对称,∴OC⊥
关于直线y=2x对称,∴OC⊥![]() ,
,![]() =AD.
=AD.
∵OA=5,AC=10,∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,
∵∠![]() +∠
+∠![]() =90°,∠ACD+∠
=90°,∠ACD+∠![]() =90°,
=90°,
∴∠![]() =∠ACD.
=∠ACD.
又∵∠![]() =∠OAC=90°,
=∠OAC=90°,
∴![]() ∽
∽![]() .
.
∴![]() 即
即![]() .
.
∴![]() =4,AE=8.
=4,AE=8.
∴OE=AE-OA=3.
∴点A/的坐标为(﹣3,4).
当x=﹣3时, ![]() .
.
所以,点A/在该抛物线上.
(3)存在.
理由:设直线![]() 的解析式为y=kx+b,
的解析式为y=kx+b,
则![]() ,
,
解得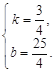
∴直线![]() 的解析式为
的解析式为![]() .
.
设点P的坐标为![]() ,则点M为
,则点M为![]() .
.
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴![]() .
.
解得![]() (不合题意,舍去)当x=2时,
(不合题意,舍去)当x=2时,![]() .
.
∴当点P运动到![]() 时,四边形PACM是平行四边形.
时,四边形PACM是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
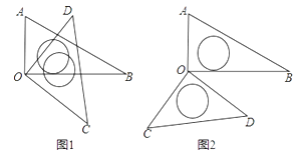
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数。
(2)如图(2)若∠AOC=140°,求∠BOD的度数
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】教材中,在计算如图1所示的正方形ABCD的面积时,分别从两个不同的角度进行了操作:
(1)把它看成是一个大正方形,则它的面积为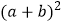 ;
;
(2)把它看成是2个小长方形和2个小正方形组成的,则它的面积为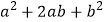 ;因此,可得到等式:
;因此,可得到等式: 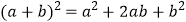 .
.
① 类比教材中的方法,由图2中的大正方形可得等式:
.
② 试在图2右边空白处画出面积为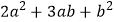 的长方形的示意图(标注好a、b),由图形可知,多项式
的长方形的示意图(标注好a、b),由图形可知,多项式 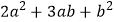 可分解因式为:
可分解因式为:
.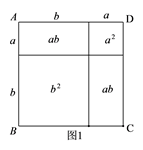
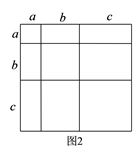
在上方空白处画出②中的示意图
③ 若将代数式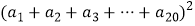 展开后合并同类项,得到多项式N,则多项式N的项数一共有项.
展开后合并同类项,得到多项式N,则多项式N的项数一共有项. -
科目: 来源: 题型:
查看答案和解析>>【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将抛物线y=﹣2(x﹣1)2+3向下平移2个单位后所得抛物线的表达式为( )
A. y=﹣2(x+1)2+3B. y=﹣2(x﹣3)2+3
C. y=﹣2(x﹣1)2+5D. y=﹣2(x﹣1)2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1).
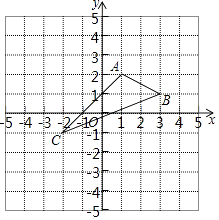
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1 .
(2)写出点A1 , B1 , C1的坐标(直接写答案)
A1
B1
C1
(3)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
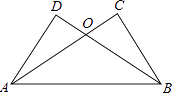
求证:
(1)BC=AD;
(2)△OAB是等腰三角形.
相关试题

