【题目】如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件_________时,可根据“ASA”判定;当添加条件_____时,可根据“AAS”判定;当添加条件________时,可根据“SAS”判定.

参考答案:
【答案】∠BCA=∠DCE(答案不唯一,也可以是∠BCD=∠ECA)∠A=∠EAB=ED
【解析】
由于BC是∠B与∠ACB的夹边,DC是∠D与∠ECD的夹边,∠B=∠D,BC=DC,要通过“ASA”判定△ABC≌△EDC,只需∠ACB=∠ECD即可;由于BC是∠A的对边,DC是∠E的对边,∠B=∠D,BC=DC,要通过“AAS”判定△ABC≌△EDC,只需∠A=∠E即可;由于∠B是BC与AB的夹角,∠D是DC与DE的夹角,∠B=∠D,BC=DC,要通过“SAS”判定△ABC≌△EDC,只需AB=ED即可.
由于BC是∠B与∠ACB的夹边,DC是∠D与∠ECD的夹边,∠B=∠D,BC=DC,要通过“ASA”判定△ABC≌△EDC,只需∠ACB=∠ECD即可;
由于BC是∠A的对边,DC是∠E的对边,∠B=∠D,BC=DC,要通过“AAS”判定△ABC≌△EDC,只需∠A=∠E即可;
由于∠B是BC与AB的夹角,∠D是DC与DE的夹角,∠B=∠D,BC=DC,要通过“SAS”判定△ABC≌△EDC,只需AB=ED即可.
故答案为:∠BCA=∠DCE(答案不唯一,也可以是∠BCD=∠ECA);∠A=∠E;AB=ED.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次
第一档
第二档
第三档
每月用电量x(度)
0<x≤140
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF=
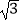 ,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒
,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒 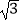 个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
(1)当△E1F1G1的顶点G1恰好在BD上时,t=秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0°<α<180°)得到△E2F2G1 , 点E1、F1分别对应E2、F2 , 设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】张老师驾车从家出发到植物园赏花,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后加速行驶,到达植物园,参观结束后,张老师驾车一路匀速返回,其中x表示汽车从家出发后所用时间,y表示车离家的距离,下面能反映y与x的函数关系式的大致图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB⊥BE于点B,DE⊥BE于点E.
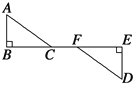
(1)若∠A=∠D,AB=DE,则△ABC与△DEF全等的理由是____;
(2)若∠A=∠D,BC=EF,则△ABC与△DEF全等的理由是_________;
(3)若AB=DE,BC=EF,则△ABC与△DEF全等的理由是_______;
(4)若AB=DE,AC=DF,则△ABC与△DEF全等的理由是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,﹣
 ,
,  ,1,3五个数中任选1个数,记为a,它的倒数记为b,将a,b代入不等式组
,1,3五个数中任选1个数,记为a,它的倒数记为b,将a,b代入不等式组  中,能使不等式组至少有两个整数解的概率是 .
中,能使不等式组至少有两个整数解的概率是 .
相关试题

