
【题目】(教材呈现)
下图是华师版九年级上册数学教材第79页的部分内容.
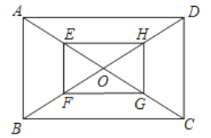
如图,矩形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
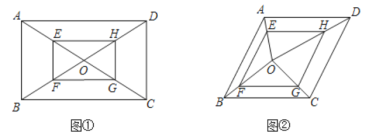
请根据教材内容,结合图①,写出完整的解题过程.
(结论应用)
(1)在图①中,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为__________;
的面积为__________;
(2)如图②,在菱形![]() 中,
中,![]() ,
,![]() 是其内任意一点,连接
是其内任意一点,连接![]() 与菱形
与菱形![]() 各顶点,四边形
各顶点,四边形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 、
、![]() 上,
上,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 与
与![]() 的面积和为
的面积和为![]() ,则菱形
,则菱形![]() 的周长为___________.
的周长为___________.
【答案】证明见解析;(1)![]() ;(2)24
;(2)24
【解析】
由矩形的性质得出OA=OC=OB=OD,再证出OE=OF=OG=OH,即可得出结论.
(1)证明△OEF为等边三角形,得出∠EFO=60°,可求出![]() ,则答案即可求出;
,则答案即可求出;
(2)过点G作GN⊥EF于点N,由条件可知四边形EFGH为平行四边形,可得∠EFG=60°,设![]() ,则
,则![]() ,由
,由![]() 与
与![]() 的面积和为
的面积和为![]() 可列出方程求出x,证明
可列出方程求出x,证明![]() ,可得
,可得![]() ,可求出AB的长,则答案可求出.
,可求出AB的长,则答案可求出.
解:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∵![]() ,
,
∴四边形![]() 是矩形.
是矩形.
(1)解:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 的面积为
的面积为![]() ,
,
故答案为:![]() .
.
(2)过点![]() 作
作![]() 于点
于点![]() ,
,
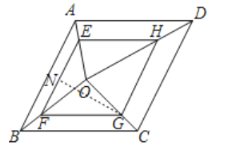
∵![]() ,且
,且![]()
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() 与
与![]() 的面积和为
的面积和为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴菱形![]() 的周长为24.
的周长为24.
故答案为:24.


科目:初中数学 来源: 题型:
【题目】小张同学尝试运用课堂上学到的方法,自主研究函数y=![]() 的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 自变量的取值范围是 ;
自变量的取值范围是 ;
(2)下表列出了y与x的几组对应值:
x | … | ﹣2 | ﹣ | m | ﹣ | ﹣ |
|
| 1 |
| 2 | … |
y | … |
|
| 1 |
| 4 | 4 |
| 1 |
|
| … |
表中m的值是 ;
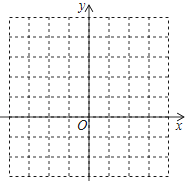
(3)如图,在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图象;
(4)结合函数y=![]() 的图象,写出这个函数的性质: .(只需写一个)
的图象,写出这个函数的性质: .(只需写一个)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象过点A(-2,0),B(4,0),C(0,4)
(1)求二次函数的解析式;
(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标,若不存在,请说明理由.
(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角![]() ,且tan
,且tan![]() =
=![]() ,求点K的坐标.
,求点K的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知轮船甲在A处沿北偏东65°的方向匀速航行,同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行,速度与甲轮船的速度相同.若经过一段时间后,两艘轮船恰好相遇,则轮船乙的航行方向为( )
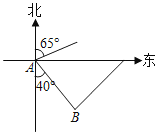
A.北偏西40°B.北偏东40°C.北偏西35°D.北偏东35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
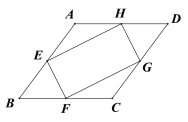
A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片![]() 沿过点
沿过点![]() 的直线折叠,使得点
的直线折叠,使得点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ;再将
;再将![]() 分别沿
分别沿![]() 折叠,此时点
折叠,此时点![]() 落在
落在![]() 上的同一点
上的同一点![]() 处.请完成下列探究:
处.请完成下列探究:
![]() 的大小为__________
的大小为__________![]() ;
;
![]() 当四边形
当四边形![]() 是平行四边形时
是平行四边形时![]() 的值为__________.
的值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年植树节期间,某景观园林公司购进一批成捆的![]() ,
,![]() 两种树苗,每捆
两种树苗,每捆![]() 种树苗比每捆
种树苗比每捆![]() 种树苗多10棵,每捆
种树苗多10棵,每捆![]() 种树苗和每捆
种树苗和每捆![]() 种树苗的价格分别是630元和600元,而每棵
种树苗的价格分别是630元和600元,而每棵![]() 种树苗和每棵
种树苗和每棵![]() 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵,![]() 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进
种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进![]() 种树苗和
种树苗和![]() 种树苗各多少棵?并求出最低费用.
种树苗各多少棵?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段![]() 分为两线段
分为两线段![]() ,
,![]() ,使得其中较长的一段
,使得其中较长的一段![]() 是全长
是全长![]() 与较短的段
与较短的段![]() 的比例中项,即满足
的比例中项,即满足![]() ,后人把
,后人把![]() 这个数称为“黄金分割”数,把点G称为线段
这个数称为“黄金分割”数,把点G称为线段![]() 的“黄金分割”点.如图,在
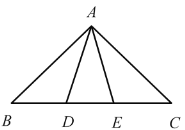
的“黄金分割”点.如图,在![]() 中,已知
中,已知![]() ,
,![]() ,若D,E是边
,若D,E是边![]() 的两个“黄金分割”点,则
的两个“黄金分割”点,则![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
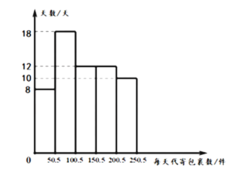
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com