【题目】
(1)如图1,四边形ABCD是正方形,点E、点F分别在边AB和AD上,且AE=AF.此时,线段BE、DF的数量关系是 , 位置关系是 . 请直接写出结论.
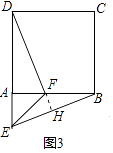
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.
(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当α=90°时,连接BE、DF,若正方形的边长为1,猜想当AE=时,直线DF垂直平分BE.请写出计算过程.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论: .
参考答案:
【答案】
(1)BE=DF;BE⊥DF
(2)
中的结论仍然成立.
理由:如图2中,延长DF交BE于H.
∵四边形ABCD是正方形,
∴AD=AB,AF=AE,∠DAB=∠FAE=90°,
在△DAF和△BAE中,
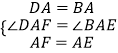 ,
,
∴△DAF≌△BAE,
∴DF=BE,∠ADF=∠ABR,
∵∠AFD=∠BFH,
∴∠DAF=∠BHF=90°,
∴DF⊥BE
(3)![]() ﹣1
﹣1
(4)正方形
【解析】解:(1.)如图1中,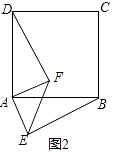
∵四边形ABCD是正方形,
∴∠DAB=90°,AD=AB,
∵AF=AE,
∴BE=DF,BE⊥DF,
所以答案是BE=DF,BE⊥DF
(3.)如图3中,连接BD.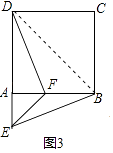
在Rt△ABD中,∵AD=AB=1,
∴BD= ![]() =
= ![]() ,
,
∵DF垂直平分线段EB,
∴DE=DB= ![]() ,
,
∴AE=DE﹣AD= ![]() ﹣1,
﹣1,
所以答案是 ![]() ﹣1.
﹣1.
(4.)如图4中,设M、N、G、H分别是BD、DE、EF、BF的中点,连接BE,DF,MN,NG,GH,HM.EB交DF于O,MN交DF于P.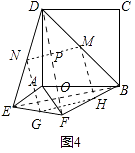
易证:DF=EB,DF⊥EB,
∵DN=NE,DM=MB,
∴MN∥EB,MN= ![]() EB,同理可证GH∥EB,GH=
EB,同理可证GH∥EB,GH= ![]() EB,MH∥DF,MH=
EB,MH∥DF,MH= ![]() DF,GN∥DF,GN=
DF,GN∥DF,GN= ![]() DF,
DF,
∴MN=NG=GH=HM,
∴四边形MNGH是菱形,
∵MN∥EB,
∴∠DPM=∠DOB=90°,
∵DF∥MH,
∴∠NMH=∠DPM=90°,
∴四边形MNGH是正方形.
所以答案是正方形
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若某几何体从某个方向观察得到的视图是正方形,则这个几何体可以是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥的主视图是边长为4cm的等边三角形,则该圆锥侧面展开图的面积是cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为

A. 2 B.
 C. 4 D.
C. 4 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿ABCM运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
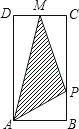
A.
B.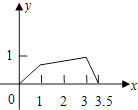
C.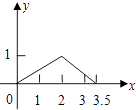
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对数字1.8045进行四舍五入取近似数,精确到0.01的结果为( )
A. 1.8B. 1.80C. 1.81D. 1.805
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+mx+n分解因式的结果是(x+2)(x﹣1),则m+n的值为_____.
相关试题

