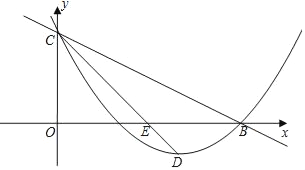
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
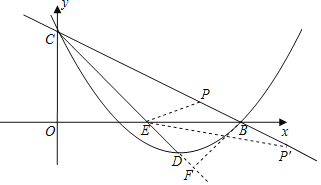
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
参考答案:
【答案】(1)D(4,﹣1);(2)![]() ;(3)点P(
;(3)点P(![]() ,
,![]() )或(12,﹣3).
)或(12,﹣3).
【解析】分析:(1)直接利用待定系数法求出二次函数解析式进而得出答案;
(2)利用锐角三角函数关系得出EC,BF的长,进而得出答案;
(3)分别利用①点P在x轴上方,②点P在x轴下方,分别得出点P的坐标.
详解:(1)由题意得B(6,0),C(0,3),
把B(6,0)C(0,3)代入y=ax2-2x+c
得![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=![]() x2-2x+3
x2-2x+3
=![]() (x2-8x)+3
(x2-8x)+3
=![]() (x-4)2-1,
(x-4)2-1,
∴D(4,-1);
(2)可得点E(3,0),
OE=OC=3,∠OEC=45°,
过点B作BF⊥CD,垂足为点F
在Rt△OEC中,EC=![]() ,
,
在Rt△BEF中,BF=BEsin∠BEF=![]() ,
,
同理,EF=![]() ,
,
∴CF=![]() +
+![]() =
=![]() ,
,
在Rt△CBF中,tan∠BCD=![]() ;
;
(3)设点P(m,![]() m+3)
m+3)
∵∠PEB=∠BCD,
∴tan∠PEB=tan∠BCD=![]() ,
,
①点P在x轴上方
∴![]() ,
,
解得:m=![]() ,
,
∴点P(![]() ,
,![]() ),
),
②点P在x轴下方
∴![]() ,
,
解得:m=12,
∴点P(12,-3),
综上所述,点P(![]() ,
,![]() )或(12,-3).
)或(12,-3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点
 从
从 出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点
出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点 第
第 次碰到矩形的边时,点
次碰到矩形的边时,点 的坐标为( )
的坐标为( )
A. (0,3) B. (5,0) C. (1,4) D. (8,3)
-
科目: 来源: 题型:
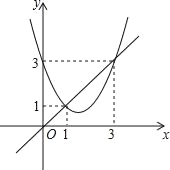
查看答案和解析>>【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
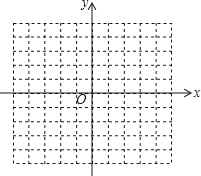
查看答案和解析>>【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为使学生及时穿上合身的校服,现提前对该校八年级四班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为 6 个型号)

根据以上信息,解答下列问题(请写出每个空所需的求解步骤)
(1)该班共有多少名学生?其中穿 175 型号校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整;(提醒:有两处需要补充)
(3)在扇形统计图中,185 型校服所对应的扇形圆心角的大小是 度;
(4)该班学生所穿校服型号的众数是 型,中位数是 型。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富居民业余生活,某居民区组建筹委会,该筹委会动员居民自愿集资建立一个书刊阅览室.经预算,一共需要筹资30 000元,其中一部分用于购买书桌、书架等设施,另一部分用于购买书刊.
(1)筹委会计划,购买书刊的资金不少于购买书桌、书架等设施资金的3倍,问最多用多少资金购买书桌、书架等设施?
(2)经初步统计,有200户居民自愿参与集资,那么平均每户需集资150元.镇政府了解情况后,赠送了一批阅览室设施和书籍,这样,只需参与户共集资20 000元.经筹委会进一步宣传,自愿参与的户数在200户的基础上增加了a%(其中
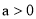 ).则每户平均集资的资金在150元的基础上减少了
).则每户平均集资的资金在150元的基础上减少了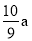 %,求a的值.
%,求a的值.
相关试题

