【题目】大家已经知道,完全平方公式和平方差公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:2x(x+y)=2x2+2xy就可以用图的面积表示.
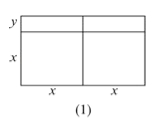
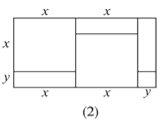
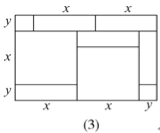
(1)请写出图(2)所表示的代数恒等式: _______ ;
(2)请写出图(3)所表示的代数恒等式: ________ ;
(3)试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x2+4xy+3y2.
参考答案:
【答案】(1)2x2+3xy+y2 (2)(x+2y)(2x+y)=2x2+5xy+2y2 (3)x2+4xy+3y2
【解析】
试题分析:(1)图(2)中,大长方形边长为(x+y),(2x+y),图形中包括了两个边长为x的正方形,三个边长为x、y的长方形,一个边长为y的正方形,根据面积关系得出代数恒等式;
(2)图(3)中,大长方形边长为(x+2y),(2x+y),图形中包括了两个边长为x的正方形,五个边长为x、y的长方形,二个边长为y的正方形,根据面积关系得出代数恒等式;
(3)根据题意,画出边长为(x+y),(x+3y)的长方形,再将图形划分,利用面积关系说明等式.
解:(1)由图(2)的面积关系可知,(x+y)(2x+y)=2x2+3xy+y2;
故答案为:2x2+3xy+y2;
(2)由图(3)的面积关系可知,(x+2y)(2x+y)=2x2+5xy+2y2;
故答案为:(x+2y)(2x+y)=2x2+5xy+2y2;
(3)以边长为(x+y),(x+3y)画长方形,如图所示,

由图可知,(x+y)(x+3y)=x2+4xy+3y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线G1:y=ax2+bx+c的顶点为(2,﹣3),且经过点(4,1).
(1)求抛物线G1的解析式;
(2)将抛物线G1先向左平移3个单位,再向下平移1个单位后得到抛物线G2 , 且抛物线G2与x轴的负半轴相交于A点,求A点的坐标;
(3)如果直线m的解析式为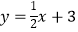 ,点B是(2)中抛物线G2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n过点A和点B.问:是否存在点B,使直线m、n、x轴围成的三角形和直线m、n、y轴围成的三角形相似?若存在,求出点B的坐标;若不存在,请说明理由.
,点B是(2)中抛物线G2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n过点A和点B.问:是否存在点B,使直线m、n、x轴围成的三角形和直线m、n、y轴围成的三角形相似?若存在,求出点B的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,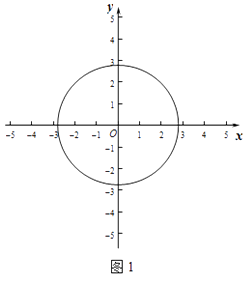
如果⊙O的半径为 ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.

(1)求证:△COM∽△CBA;
(2)求线段OM的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1, 在
 中,
中,  ,
,  .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为  ,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P为∠ACB平分线上的一点,∠ACB=60°,PD⊥CA于D,PE⊥CB于E,点M是线段CP上的一动点(不与两端点C,P重合),连接DM,EM.
(1)求证:DM=EM;
(2)当点M运动到线段CP的什么位置时,四边形PDME为菱形,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为米.

相关试题

