【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为米.
参考答案:
【答案】11.5
【解析】由题意得:∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
则 ![]() ,即
,即 ![]()
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m),
即旗杆的高度为11.5m;
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家已经知道,完全平方公式和平方差公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:2x(x+y)=2x2+2xy就可以用图的面积表示.
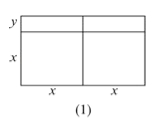
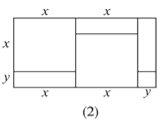
(1)请写出图(2)所表示的代数恒等式: _______ ;
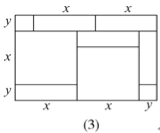
(2)请写出图(3)所表示的代数恒等式: ________ ;
(3)试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x2+4xy+3y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1, 在
 中,
中,  ,
,  .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为  ,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P为∠ACB平分线上的一点,∠ACB=60°,PD⊥CA于D,PE⊥CB于E,点M是线段CP上的一动点(不与两端点C,P重合),连接DM,EM.
(1)求证:DM=EM;
(2)当点M运动到线段CP的什么位置时,四边形PDME为菱形,请说明理由.

-
科目: 来源: 题型:
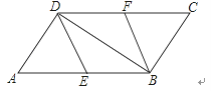
查看答案和解析>>【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如:下问题
尺规作图:过圆外一点作园的切线
已知:圆O和点P
求作:过点P的圆O的切线
小涵的主要作法如下:
如图:①连接OP,作线段OP的中点A
②以A为圆心,OA长为半径作圆,交圆O于点B,C
③作直线PB和PC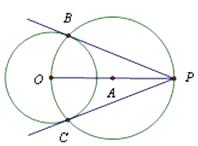
所以PB和PC就是所求的切线
老师说:“小涵的作法正确.”
请回答:小涵的作图依据是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它是一个长为2m,宽为2n的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形边长为
(2)请用两种不同的方法表示图(2)阴影部分的面积;
方法一: 方法二:
(3)观察图(2),写出三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系.
(4)根据(3)题中的等量关系,解决下列问题:若a+b=7,ab=5,求(a﹣b)2的值.

相关试题

