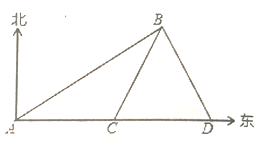
【题目】如图所示,李师傅开着汽车在公路上行驶到A处时,高塔B在A的北偏东60![]() 方向上,李师傅以每分钟125米的速度向东行驶,到达C处时,高塔B在C的北偏东30
方向上,李师傅以每分钟125米的速度向东行驶,到达C处时,高塔B在C的北偏东30![]() 方向上,到达D处时,高塔B在D的北偏西30
方向上,到达D处时,高塔B在D的北偏西30![]() 方向上,当汽车到达D处时恰与高塔B相距500米.
方向上,当汽车到达D处时恰与高塔B相距500米.
(1)判断△BCD的形状:
(2)求汽车从A处到达D处所需要的时间:(3)若汽车从A处向东行驶6分钟到达E处,请你直接写出此时高塔B在E的什么方向上?
参考答案:
【答案】(1)△BCD是等边三角形(2)汽车从A处到达D处所需要的时间为8分钟(3)高塔B在E的正北方向上
【解析】试题分析:(1)根据题意得出∠BCD=∠BDC=60°,即可得出△BCD的形状;
(2)根据三角形外角的性质以及等边三角形的性质得出AD的长,进而求出答案;
(3)根据题意求出AE的长,再利用等腰三角形的性质得出B,E的位置关系.
试题解析:解:(1)由题意可得:
∠4=∠5=30°,则∠BCD=∠BDC=60°,故△BCD是等边三角形;
(2)∵△BCD是等边三角形,BD=500m,∴BC=CD=500m,∵∠2=90°﹣∠1=30°,∠BCD=60°,∴∠3=30°,∴AC=BC=500m,∴AD=1000m,∴1000÷125=8(分钟),答:汽车从A处到达D处所需要8分钟;
(3)∵汽车从A处向东行驶6分钟到达E处,∴AE=125×6=750(m),则CE=250m,故E为CD的中点,则BE⊥CD,即高塔B在E的正北方向.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜全面调查的是( )
A. 调查市场上某种食品的色素含量是否符合国家标准 B. 了解我国七年级学生的身高情况
C. 调查春节联欢晚会的收视率 D. 选出某校短跑最快的学生参加全市比赛
-
科目: 来源: 题型:
查看答案和解析>>【题目】把函数y=2x2的图象先向右平移3个单位长度,再向下平移2个单位长度得到新函数的图象,则新函数的表达式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,我省2019年生产总值约为37100亿元,其中“37100亿”用科学记数法表示为( )
A.3.71×1012B.3.71×1011C.0.371×105D.3.71×104
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E、F,当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证
 .
. 当∠EDF绕
当∠EDF绕 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立, 、
、 、
、 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
-
科目: 来源: 题型:
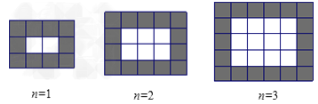
查看答案和解析>>【题目】如图,用相同规格的黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题:
(1)在第n个图中,共有瓷砖______________________块,其中白色瓷砖______________块,
黑色瓷砖_________________块(均用含n的代数式表示)
(2)按上述铺设方案,铺设一块这样的矩形地面共用了1056块瓷砖,求此时n的值;
(3)若黑瓷砖每块4元,白瓷砖每块3元,则问题(2)中,共花多少元购买瓷砖?
-
科目: 来源: 题型:
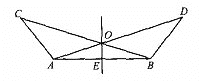
查看答案和解析>>【题目】如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.
相关试题

