【题目】某学校打算招聘英语教师。对应聘者进行了听、说、读、写的英语水平测试,其中甲、乙两名应聘者的成绩(百分制)如下表所示。

(1)如果学校想招聘说、读能力较强的英语教师,听、说、读、写成绩按照2:4:3:1的比确定,若在甲、乙两人中录取一人,请计算这两名应聘者的平均成绩(百分制)。从他们的成绩看,应该录取谁?
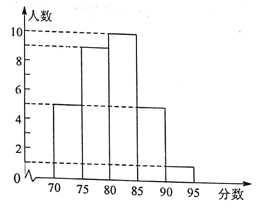
(2)学校按照(1)中的成绩计算方法,将所有应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最后左边一组分数![]() 为:
为:![]() )。
)。
①参加该校本次招聘英语教师的应聘者共有______________人(直接写出答案即可)。
②学校决定由高分到低分录用3名教师,请判断甲、乙两人能否被录用?并说明理由。
参考答案:
【答案】(1)录取乙;(2)①30,②乙一定能被录用;甲不一定能被录用,见解析.
【解析】
(1)根据加权平均数的定义与性质即可求解判断;
(2)①根据直方图即可求解;②根据直方图判断甲乙所在的分段,即可判断.
解:(1)由题意得,
![]() (分)
(分)
![]() (分)
(分)
∵![]()
∴应该录取乙。
(2)①30
②由频数分布直方图可知成绩最高一组分数段![]() 中有1人,而
中有1人,而![]() 分,所以乙是第一名,一定被录取;在
分,所以乙是第一名,一定被录取;在![]() 一组有5人,其中有2人被录用,
一组有5人,其中有2人被录用,![]() 分,可确定甲在本组中,但不能确定甲在本组中排第几名,所以甲不一定能被录用。
分,可确定甲在本组中,但不能确定甲在本组中排第几名,所以甲不一定能被录用。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>
 ;其中正确的个数为( )
;其中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,如(4,2)表示整数8.则(62,55)表示的数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备利用寒假期间走访慰问贫困家庭学生,并给每位贫困家庭学生赠送一份学习用品,学习用品每份售价60元,某商场给出了两种团购(50份以上)优惠方案:方案一:5份学习用品享受爱心免费赠送,剩下的学习用品按售价打九折;方案二:所购买的学习用品全部按售价打八五折.
(1)该校采购老师发现:该校无论选择哪种团购方案,要付的钱是一样的,问该校需要购买多少份学习用品?
(2)若该校改变计划,需购买学习用品80份,选择哪种方案优惠?说明理由,并求出选择该方案优惠的百分数(精确到1%).
-
科目: 来源: 题型:
查看答案和解析>>【题目】电话计费问题,下表中有两种移动电话计费方式:

温馨揭示:方式一:月使用费固定收(月收费:38元/月);主叫不超限定时间不再收费(80分钟以内,包括80分钟);主叫超时部分加收超时费(超过部分0.15元/
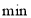 );被叫免费。
);被叫免费。方式二:月使用费0元(无月租费);主叫限定时间0分钟;主叫每分钟0.35元/
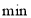 ;被叫免费。
;被叫免费。(1)设一个月内用移动电话主叫时间为
 ,方式一计费
,方式一计费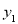 元,方式二计费
元,方式二计费 元。写出
元。写出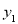 和
和 关于
关于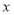 的函数关系式。
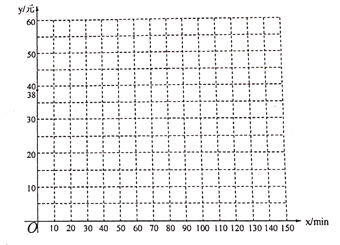
的函数关系式。(2)在平面直角坐标系中画出(1)中的两个函数图象,记两函数图象交点为点
 ,则点
,则点 的坐标为_____________________(直接写出坐标,并在图中标出点
的坐标为_____________________(直接写出坐标,并在图中标出点 )。
)。(3)根据(2)中函数图象,请直接写出如何根据每月主叫时间选择省钱的计费方式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践与探究
宽与长的比是
 (约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
(约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。下面我们通过折纸得到黄金矩形。
第一步,在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平。

第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是
 。
。第三步,折出内侧矩形的对角线
 ,并把
,并把 折到图3中所示的
折到图3中所示的 处,折痕为
处,折痕为 。
。第四步,展平纸片,按照所得的点
 折出
折出 ,使
,使 ;过点
;过点 折出折痕
折出折痕 ,使
,使 。
。
(1)上述第三步将
 折到
折到 处后,得到一个四边形
处后,得到一个四边形 ,请判断四边形
,请判断四边形 的形状,并说明理由。
的形状,并说明理由。(2)上述第四步折出折痕
 后得到一个四边形
后得到一个四边形 ,这个四边形是黄金矩形,请你说明理由。(提示:设
,这个四边形是黄金矩形,请你说明理由。(提示:设 的长度为2)
的长度为2)(3)在图4中,再找出一个黄金矩形_______________________________(黄金矩形
 除外,直接写出答案,不需证明,可能参考数值:
除外,直接写出答案,不需证明,可能参考数值: )
)(4)请你举一个采用了黄金矩形设计的世界名建筑_________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践与探究
如图,在平面直角坐标系中,直线
 交
交 轴于点
轴于点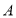 ,交
,交 轴于点
轴于点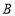 ,点
,点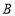 坐标为
坐标为 。直线
。直线 与直线
与直线 相交于点
相交于点 ,点
,点 的横坐标为1。
的横坐标为1。(1)求直线
 的解析式;
的解析式;(2)若点
 是
是 轴上一点,且
轴上一点,且 的面积是
的面积是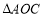 面积的
面积的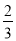 ,求点
,求点 的坐标;
的坐标;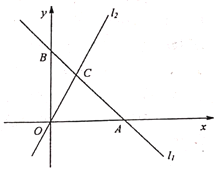
相关试题

