练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在正方形网格中，每个小正方形的边形为1个单位长度，线段AD的两个端点都在格点上，点B是线段AD上的格点，且BD=1，直线l在格线上.

    （1）在直线l的左侧找一格点C，使得△ABC是等腰三角形（AC＜AB）,画出△ABC.

    （2）将△ABC沿直线l翻折得到△，试画出△.

    （3）画出点P，使得点P到点D、A’的距离相等，且到边AB、AA’的距离相等.

    【答案】见解析

    【解析】

    （1）根据等腰三角形的性质及勾股定理找出点C即可；
    （2）分别作出各点关于直线l的对称点，再顺次连接即可；
    （3）作线段A′D的垂直平分线与∠BAA′的平分线，两直线的交点即为P点．

    （1）如图，点C为所作点；


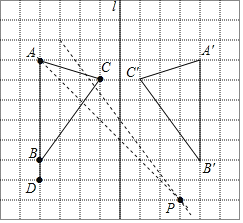
    （2）如图，△A′B′C′为所作三角形；
    （3）如图，点P为所作点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，过点的直线与直线相交于点，动点在线段和射线上运动.

    （1）求直线的函数关系式.

    （2）求的面积.

    （3）是否存在点，使的面积与的面积相等？若存在求出此时点的坐标；若不存在，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（11·湖州）如图，已知抛物线经过点（0，－3），请你确定一个

    b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间。你确定的b的值是 ▲ 。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠C=90°，E为AB中点，D为AC上一点，BF//AC交DE的延长线长于点F，AC=6，BC=5.则四边形FBCD周长的最小值是（ ）

    A.21B.16C.17D.15

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，CD=5，DA=，则BD的长为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=5cm，BC=3cm，AC=4cm，若动点P从点C开始，按照C→A→B的路径运动，且运动速度为每秒2cm，设出发的时间为t秒.

    （1）请判断△ABC的形状，说明理由

    （2）当t为何值时，△BCP是以BC为腰的等腰三角形，求出t的值

    （3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒1cm，若P、Q两点同时出发， 当P、Q中有一点到达终点时，另一点也停止运动，当t为何值时，P、Q两点之间的距离为，直接写出t的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

    （1）在图中的点上标出相应字母A、B、C，并求出△ABC的面积；

    （2）在图中作出△ABC关于y轴的对称图形△A1B1C1；

    （3）写出点A1，B1，C1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于一元二次方程（，，，为常数），下列说法：

    ①方程的解为；

    ②若，则方程必有一根为；

    ③若，则一元二次方程必有一根为；

    ④若，则方程有两个不等实数根；

    ⑤若，则方程有两个相等的实数根，

    正确的结论是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，平分交于点，则

    A. B. C. D. 或

    查看答案和解析>>

    同步练习册答案