【题目】计算(1)![]()
(2)计算![]() ,嘉嘉同学的计算过程如下:
,嘉嘉同学的计算过程如下:
原式![]()
请你判断嘉嘉的计算过程是否正确,若不正确,请写出正确的计算过程.
(3)定义一种运算:观察下列各式:![]() ,
,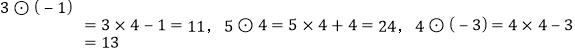 .
.
①请你想一想:![]() .
.
②若![]() ,那么
,那么![]()
![]() (
(![]() 填或
填或![]() )
)
③先化简,在求值:![]() 其中
其中![]() .
.
参考答案:
【答案】(1)![]() ;(2)嘉嘉的计算过程不正确,-36;(3)①
;(2)嘉嘉的计算过程不正确,-36;(3)①![]() ; ②
; ②![]() ;③
;③![]() ,0.
,0.
【解析】
(1)(2)根据有理数的混合运算法则计算即可.
(3)①根据题目中的式子可以猜出a⊙b的结果;
②根据①中的结果和a≠b,可以得到a⊙b和b⊙a的关系;
③根据①中的结果可以化简(a﹣b)⊙(2a+b),代入求值即可.
(1)原式=![]() =
=![]() =
=![]() ;
;
(2)嘉嘉的计算过程不正确.正确的计算过程如下:
原式![]()
![]() ;
;
(3)①由题目中的式子可得:a⊙b=4a+b.
故答案为:4a+b;
②∵a⊙b=4a+b,b⊙a=4b+a,∴(a⊙b)﹣(b⊙a)
=(4a+b)﹣(4b+a)
=4a+b﹣4b﹣a
=3(a﹣b).
∵a≠b,∴3(a﹣b)≠0,∴(a⊙b)≠(b⊙a).
故答案为:≠;
(3)(a﹣b)⊙(2a+b)
=4(a﹣b)+(2a+b)
=4a﹣4b+2a+b
=6a﹣3b
当a=1,b=2时,原式=6×1-3×2=6-6=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为(单位:环):
甲:8,8,7,8,9
乙:5,9,7,10,9
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手
平均数
众数
中位数
方差
甲
8
b
8
0.4
乙
α
9
c
3.2
根据以上信息,请解答下面的问题:
(1)α= ,b= ,c= ;
(2)完成图中表示乙成绩变化情况的折线;
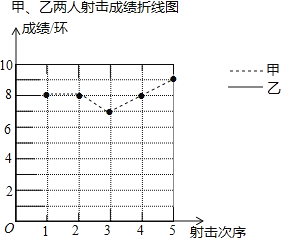
(3)教练根据这5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(4)若选手乙再射击第6次,命中的成绩是8环,则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会 .(填“变大”、“变小”或“不变”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高
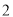 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心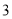 米.
米.
(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
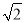 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;当n=3时,钉子板上所连不同线段的长度值只有1,
 ,2,
,2,  ,2
,2 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.(1)观察图形,填写下表:
钉子数(n×n)
S值
2×2
2
3×3
2+3
4×4
2+3+(____)
5×5
(________)
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售每台A型电脑的利润为100元,销售每台B型电脑的利润为150元,该商店计划一次购进A,B两种型号的电脑共100台,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y与x的函数关系式;
(2)该商店计划一次购进A,B两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,那么商店购进A型、B型电脑各多少台,才能使销售总利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图像可能是 ( )
A.
 B.
B. 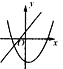 C.
C. 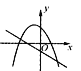 D.
D. 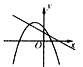
相关试题

