【题目】某商店销售每台A型电脑的利润为100元,销售每台B型电脑的利润为150元,该商店计划一次购进A,B两种型号的电脑共100台,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y与x的函数关系式;
(2)该商店计划一次购进A,B两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,那么商店购进A型、B型电脑各多少台,才能使销售总利润最大?
参考答案:
【答案】(1)y=﹣50x+15000;(2)商店购进A型34台、B型电脑66台,才能使销售总利润最大.
【解析】
(1)根据总利润等于A、B电脑利润相加可以求得y与x的函数关系式,从而可以解答本题;
(2)根据题意和B型电脑的进货量不超过A型电脑的2倍,可以求得x的取值范围,再根据一次函数的性质即可解答本题.
解:(1)由题意可得,
y=100x+150(100﹣x)=﹣50x+15000,
即y与x的函数关系式是y=﹣50x+15000;
(2)由题意可得,
100﹣x≤2x,解得,x≥![]() ,
,
∵y=﹣50x+15000,
∴当x=34时,y取得最大值,此时y=13300,100﹣x=66,
即商店购进A型34台、B型电脑66台,才能使销售总利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高
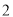 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心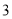 米.
米.
(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(1)
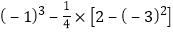
(2)计算
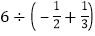 ,嘉嘉同学的计算过程如下:
,嘉嘉同学的计算过程如下:原式
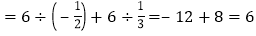
请你判断嘉嘉的计算过程是否正确,若不正确,请写出正确的计算过程.
(3)定义一种运算:观察下列各式:
 ,
,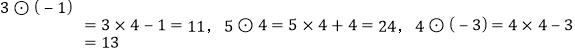 .
.①请你想一想:
 .
.②若
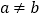 ,那么
,那么
 (
(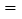 填或
填或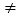 )
)③先化简,在求值:
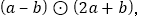 其中
其中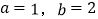 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
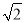 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;当n=3时,钉子板上所连不同线段的长度值只有1,
 ,2,
,2,  ,2
,2 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.(1)观察图形,填写下表:
钉子数(n×n)
S值
2×2
2
3×3
2+3
4×4
2+3+(____)
5×5
(________)
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图像可能是 ( )
A.
 B.
B. 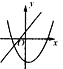 C.
C. 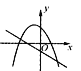 D.
D. 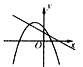
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师设计了一个数学实验,给甲、乙、丙三名同学各一张写有已化为最简(没有同类项)的代数式的卡片,规则是两位同学的代数式相减等于第三位同学的代数式,则实验成功,甲、乙、丙的卡片如下,丙的卡片有一部分看不清楚了.
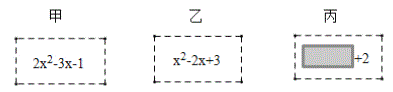
(1)计算出甲减乙的结果,并判断甲减乙能否使实验成功;
(2)嘉琪发现丙减甲可以使实验成功,请求出丙的代数式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=
 AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )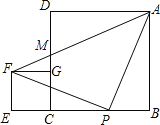
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
相关试题

