【题目】如图,已知AD是三角形纸片ABC的高,将纸片沿直线EF折叠,使点A与点D重合,给出下列判断: ①EF是△ABC的中位线;
②△DEF的周长等于△ABC周长的一半;
③若四边形AEDF是菱形,则AB=AC;
④若∠BAC是直角,则四边形AEDF是矩形,
其中正确的是( )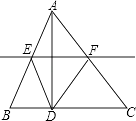
A.①②③
B.①②④
C.②④
D.①③④
参考答案:
【答案】A
【解析】解:∵AD是△ABC的高, ∴AD⊥BC,
∴∠ADC=90°,
根据折叠可得:EF是AD的垂直平分线,
∴AO=DO= ![]() AD,AD⊥EF,
AD,AD⊥EF,
∴∠AOF=90°,
∴∠AOF=∠ADC=90°,
∴EF∥BC,
∴△AEF∽△ABC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴EF是△ABC的中位线,
故①正确;
∵EF是△ABC的中位线,
∴△AEF的周长是△ABC的一半,
根据折叠可得△AEF≌△DEF,
∴△DEF的周长等于△ABC周长的一半,
故②正确;
∵EF是△ABC的中位线,
∴AE= ![]() AB,AF=
AB,AF= ![]() AC,
AC,
若四边形AEDF是菱形,
则AE=AF,
∴AB=AC,
故③正确;
根据折叠只能证明∠BAC=∠EDF=90°,
不能确定∠AED和∠AFD的度数,故④错误;
故选:A.
【考点精析】本题主要考查了三角形中位线定理和菱形的性质的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 .

(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示的块,块,块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式:(1)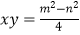 (2)x+y=m(3)x2﹣y2=mn(4)
(2)x+y=m(3)x2﹣y2=mn(4) 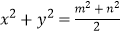 其中正确的有
其中正确的有
A.1个
B.2个
C.3个
D.4个. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面坐标系中,点P(3,4)是线段AB上一点,以原点为位似中心把△AOB扩大到原来的2倍,则点P对应的点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算-3a·2b,正确的结果是 ( )
A. -6ab B. 6ab C. -ab D. ab
-
科目: 来源: 题型:
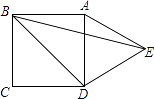
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD= .
-
科目: 来源: 题型:
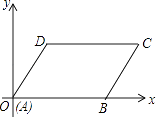
查看答案和解析>>【题目】如图,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0)、(5,0)、(2,3),则顶点C的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 为了解航天员视力的达标情况应采用抽样调查方式
B. 一组数据3,6,7,6,9的中位数是7
C. 正方体的截面形状一定是四边形
D. 400人中一定有两个人的生日在同一天是必然事件
相关试题

