【题目】阅读材料:我们知道,4x+2x-x=(4+2-1)x=5x,类似地,我们把(a+b)看成一个整体,则4(a+b)+2(a+b)-(a+b)-(4+2-1)(a+b)=5(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(a-b)看成一个整体,合并3(a-b)2-7(a-b)2+2(a-b)2的结果是____________.
(2)已知x2-2y=5,求21-![]() x2+y的值;
x2+y的值;
(3)拓广探索:已知a-2b=3,2b-c=-5,c-d=10,求2(a-c)+2(2b-d)-2(2b-c)的值.
参考答案:
【答案】(1) -2(a-b)2;(2)18![]() ;(3)16.
;(3)16.
【解析】
(1)把(ab)看做一个整体,合并即可得到结果;
(2)把(x2-2y)整体代入即可求解;
(3)原式去括号整理后,将已知等式代入计算即可求出值.
解:(1)3(a-b)2-7(a-b)2+2(a-b)2= -2(a-b)2
故答案为:-2(a-b)2;
(2)∵x2-2y=5
∴21-![]() x2+y =21-
x2+y =21-![]() (x2-2y)=21-
(x2-2y)=21-![]() =18
=18![]()
(3)∵a-2b=3,2b-c=-5,c-d=10
∴2(a-c)+2(2b-d)-2(2b-c)
= 2a - 2c + 4b - 2d - 4b + 2c
=(2a-4b)+(4b-2c)+(2c-2d)
= 2×3 +2×(-5)+2×10
= 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角三角形EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤
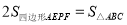 ,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)上述结论正确的是_____________.(填序号)
,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)上述结论正确的是_____________.(填序号)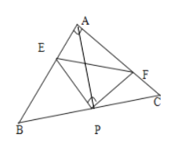
-
科目: 来源: 题型:
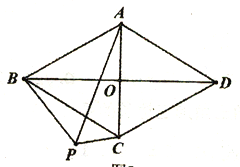
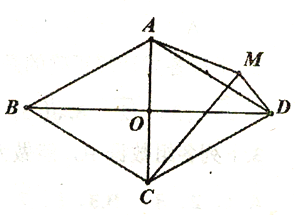
查看答案和解析>>【题目】已知在菱形ABCD中,对角线AC、BD交于点O,AB=2AO;(1)如图1,求∠BAC的度数;(2)如图2,P为菱形ABCD外一点,连接AP、BP、CP,若∠CPB=120°,求证:CP+BP=AP;(3)如图3,M为菱形ABCD外一点,连接AM、CM、DM,若∠AMD=150°,
CM=2
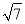 ,DM=2,求四边形ACDM的面积。
,DM=2,求四边形ACDM的面积。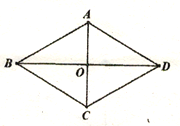
-
科目: 来源: 题型:
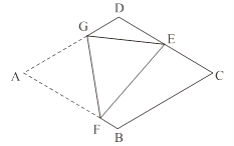
查看答案和解析>>【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为________.
-
科目: 来源: 题型:
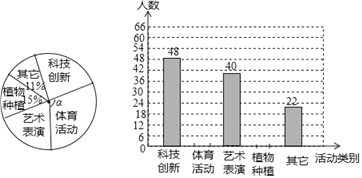
查看答案和解析>>【题目】深圳市教育局在全市中小学开展“四点半活动”试点工作,某校为了了解学生参与“四点半活动”项目的情况,对初中的部分学生进行了随机调查,调查项目分为“科技创新”类,“体育活动”类,“艺术表演”类,“植物种植”类及“其它”类共五大类别,并根据调查的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息解答下面的问题.
(1)请求出此次被调查学生的总人数 人;
(2)根据以上信息,补全频数分布直方图;
(3)求出扇形统计图中,“体育活动”α的圆心角等于 度;
(4)如果本校初中部有1800名学生,请估计参与“艺术表演”类项目的学生大约多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若线段AB=10cm,C是线段AB上的任意一点,M、N分别是AC和CB的中点,则MN= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足
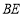 =AD,连接CE并延长交AD于点F,连接AE,过点B作
=AD,连接CE并延长交AD于点F,连接AE,过点B作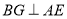 于点G,延长BG交AD于点H.在下列结论中:①
于点G,延长BG交AD于点H.在下列结论中:①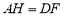 ;②
;②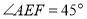 ;③
;③ . 其中不正确的结论有( )
. 其中不正确的结论有( )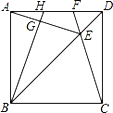
A. 0个B. 1个C. 2个D. 3个
相关试题

