【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10= . 
参考答案:
【答案】π
【解析】解:(1)图1,过点O做OE⊥AC,OF⊥BC,垂足为E、F, 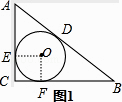
则∠OEC=∠OFC=90°
∵∠C=90°
∴四边形OECF为矩形
∵OE=OF
∴矩形OECF为正方形
设圆O的半径为r,则OE=OF=r,AD=AE=3﹣r,BD=4﹣r
∴3﹣r+4﹣r=5,r= ![]() =1
=1
∴S1=π×12=π
(2.)图2,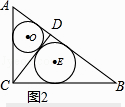
由S△ABC= ![]() ×3×4=
×3×4= ![]() ×5×CD
×5×CD
∴CD= ![]()
由勾股定理得:AD= ![]() =
= ![]() ,BD=5﹣
,BD=5﹣ ![]() =
= ![]()
由(1)得:⊙O的半径= ![]() =
= ![]() ,⊙E的半径=
,⊙E的半径= ![]() =
= ![]()
∴S1+S2=π× ![]() +π×
+π× ![]() =π
=π
(3.)图3,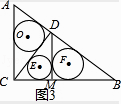
由S△CDB= ![]() ×
× ![]() ×
× ![]() =
= ![]() ×4×MD
×4×MD
∴MD= ![]()
由勾股定理得:CM= ![]() =
= ![]() ,MB=4﹣
,MB=4﹣ ![]() =
= ![]()
由(1)得:⊙O的半径= ![]() ,:⊙E的半径=
,:⊙E的半径= ![]() =
= ![]() ,:⊙F的半径=
,:⊙F的半径= ![]() =
= ![]()
∴S1+S2+S3=π× ![]() +π×
+π× ![]() +π×
+π× ![]() =π
=π
∴图4中的S1+S2+S3+S4=π
则S1+S2+S3+…+S10=π
故答案为:π.
(1)图1,作辅助线构建正方形OECF,设圆O的半径为r,根据切线长定理表示出AD和BD的长,利用AD+BD=5列方程求出半径r= ![]() (a、b是直角边,c为斜边),运用圆面积公式=πr2求出面积=π;(2)图2,先求斜边上的高CD的长,再由勾股定理求出AD和BD,利用半径r=
(a、b是直角边,c为斜边),运用圆面积公式=πr2求出面积=π;(2)图2,先求斜边上的高CD的长,再由勾股定理求出AD和BD,利用半径r= ![]() (a、b是直角边,c为斜边)求两个圆的半径,从而求出两圆的面积和=π;(3)图3,继续求高DM和CM、BM,利用半径r=
(a、b是直角边,c为斜边)求两个圆的半径,从而求出两圆的面积和=π;(3)图3,继续求高DM和CM、BM,利用半径r= ![]() (a、b是直角边,c为斜边)求三个圆的半径,从而求出三个圆的面积和=π;
(a、b是直角边,c为斜边)求三个圆的半径,从而求出三个圆的面积和=π;
综上所述:发现S1+S2+S3+…+S10=π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=
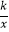 (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= 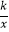 (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 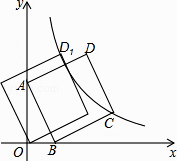
-
科目: 来源: 题型:
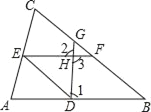
查看答案和解析>>【题目】完成下面的证明过程
如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(________),
∴∠1+∠3=180°
∴______∥______(________)
∴∠B=______(________)
∵∠B=∠DEF(已知)
∴∠DEF=______(等量代换)
∴DE∥BC(________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=
 ,BG=
,BG= ,且
,且 、
、 满足下列关系:
满足下列关系: ,
, ,则GH= .
,则GH= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,求证:PQ=
 BP.
BP.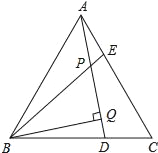
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足x12+x22=3x1x2 , 求实数p的值.
相关试题

