【题目】如图,在平面直角坐标系中,矩形OABC的边OA=6,OC=2,一条动直线l分别与BC、OA将于点E、F,且将矩形OABC分为面积相等的两部分,则点O到动直线l的距离的最大值为_____.
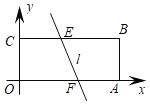
参考答案:
【答案】![]() .
.
【解析】
根据一条动直线l将矩形OABC分为面积相等的两部分,可知G和H分别是OB和OC的中点,得GH=3,根据勾股定理计算OG的长,并且知点O到直线l的距离最大,则l⊥OG,可得结论.
连接OB,交直线l交于点G,
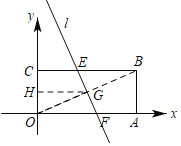
∵直线l将矩形OABC分为面积相等的两部分,
∴G是OB的中点,
过G作GH∥BC,交OC于H,
∵BC=OA=6,
∴GH=![]() BC=3,OH=
BC=3,OH=![]() OC=1,
OC=1,
若要点O到直线l的距离最大,则l⊥OG,
Rt△OGH中,由勾股定理得:OG=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
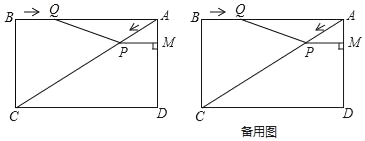
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
-
科目: 来源: 题型:
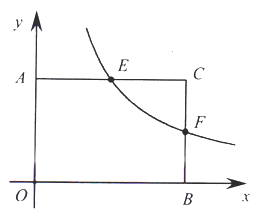
查看答案和解析>>【题目】如图,在平面直角坐标系中,
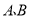 两点分别是
两点分别是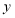 轴和
轴和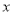 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点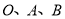 为顶点的矩形
为顶点的矩形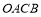 的面积为24,反比例函数
的面积为24,反比例函数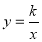 (
(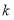 为常数且
为常数且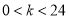 )的图象与矩形
)的图象与矩形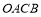 的两边
的两边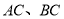 分别交于点
分别交于点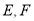 .
.
(1)若
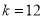 且点
且点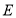 的横坐标为3.
的横坐标为3.①点
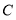 的坐标为 ,点
的坐标为 ,点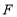 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);②在
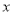 轴上是否存在点
轴上是否存在点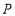 ,使
,使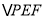 的周长最小?若存在,请求出
的周长最小?若存在,请求出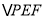 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.(2)连接
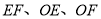 ,在点
,在点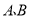 的运动过程中,
的运动过程中,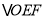 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含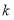 的代数式表示出
的代数式表示出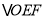 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】小强想利用树影测树高,他在某一时刻测得直立的标杆长0.8m,其影长为1m,同时测树影时因树靠近某建筑物,影子不全落在地上,有一部分落在墙上如图,若此时树在地面上的影长为5.5m,在墙上的影长为1.5m,求树高

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
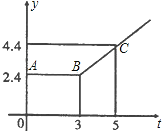
(1)写出y与t之间的函数关系式.
(2)通话2分钟应付通话费多少元?
(3)通话7分钟呢?
-
科目: 来源: 题型:
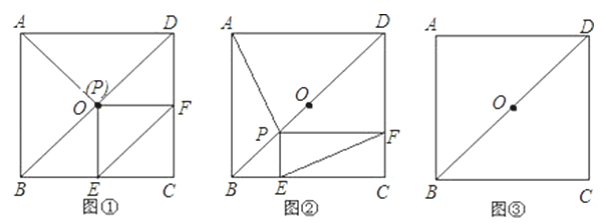
查看答案和解析>>【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.
相关试题

