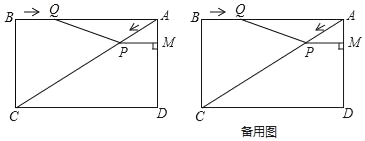
【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
参考答案:
【答案】(1)t=![]() ;(2)S四边形PQAM=﹣
;(2)S四边形PQAM=﹣![]() t2+
t2+![]() t;(3)存在t=2,使S四边形PQAM=
t;(3)存在t=2,使S四边形PQAM=![]() S矩形ABCD;(4)当t=
S矩形ABCD;(4)当t=![]() 或
或![]() 时,△APQ与△ABC相似.
时,△APQ与△ABC相似.
【解析】试题分析:(1)由点Q在线段AC的中垂线上可知CQ=AQ=8﹣2t,在Rt△BCQ中根据BC2+BQ2=CQ2列方程求解.
(2)先证明△APM∽△ACD,列方程用含t的代数式表示出AM和PM的值,然后根据四边形PQAM的面积=△APQ的面积+△APM的面积求解;
(3)存在t=2,使S四边形PQAM=![]() S矩形ABCD.首先根据四边形ABCD是矩形,求出S矩形ABCD的值是多少;然后分别求出△APM、△APQ的面积各是多少,再根据S四边形PQAM=
S矩形ABCD.首先根据四边形ABCD是矩形,求出S矩形ABCD的值是多少;然后分别求出△APM、△APQ的面积各是多少,再根据S四边形PQAM=![]() S矩形ABCD,求出t的值是多少即可.
S矩形ABCD,求出t的值是多少即可.
(4)当t=2![]() 或1
或1![]() 时,△APQ与△ABC相似.根据题意,分两种情况讨论:①当∠AQP=90°时,△APQ与△ABC相似;②当∠APQ=90°时,△APQ与△ABC相似;求出当t为何值时,△APQ与△ABC相似即可.
时,△APQ与△ABC相似.根据题意,分两种情况讨论:①当∠AQP=90°时,△APQ与△ABC相似;②当∠APQ=90°时,△APQ与△ABC相似;求出当t为何值时,△APQ与△ABC相似即可.
解:(1)由题意CQ=AQ=8﹣2t,
在Rt△BCQ中,∵BC2+BQ2=CQ2,
∴62+(2t)2=(8﹣2t)2,
解得t=![]() .
.
(2)∵四边形ABCD是矩形,
∴S矩形ABCD=ABBC=8×6=48,
∵PM⊥AD,CD⊥AD,
∴PM∥CD,
∴△APM∽△ACD,
∴![]() =
=![]() =
=![]() ,
,
即 ![]() =
=![]() =
=![]() ,
,
解得AM=![]() t,PM=
t,PM=![]() t,
t,
∴S△APM=![]() AMPM=
AMPM=![]() ×
×![]() t×
t×![]() t=
t=![]() t2.
t2.
∵sin∠PAQ=![]() =
=![]() ,
,
∴S△APQ=![]() APAQsin∠PAQ=
APAQsin∠PAQ=![]() ×2t(8﹣2t)×
×2t(8﹣2t)×![]() =
=![]() t(4﹣t),
t(4﹣t),
∵S四边形PQAM=![]() t2+
t2+![]() t(4﹣t)=﹣
t(4﹣t)=﹣![]() t2+
t2+![]() t.
t.
(3)存在t=2,使S四边形PQAM=![]() S矩形ABCD.
S矩形ABCD.
如图2,
 ,
,
∵S四边形PQAM=![]() S矩形ABCD,
S矩形ABCD,
∴![]() t2+
t2+![]() t(4﹣t)=
t(4﹣t)=![]() ×48,
×48,
整理,可得t2﹣20t+36=0
解得t=2或t=18(舍去),
∴存在t=2,使S四边形PQAM=![]() S矩形ABCD.
S矩形ABCD.
(4)当t=2![]() 或1
或1![]() 时,△APQ与△ABC相似.
时,△APQ与△ABC相似.
①当△APQ∽△ACB,
∴![]() =
=![]() ,
,
即 ![]() =
=![]() ,
,
解得t=2![]() ,
,
②如图3,
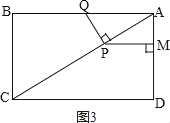 ,
,
当∠APQ=90°时,△APQ与△ABC相似,
∵tan∠PAQ=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
即 ![]() =
=![]() ,
,
∴PQ=![]() t,
t,
∵BQ=t,
∴AQ=8﹣2t,
在Rt△APQ中,
∵AP2+PQ2=AQ2,
∴(2t)2+(![]() t)2=(8﹣2t)2,
t)2=(8﹣2t)2,
解得t=1![]() 或t=﹣16(舍去).
或t=﹣16(舍去).
综上,可得
当t=2![]() 或1
或1![]() 时,△APQ与△ABC相似.
时,△APQ与△ABC相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
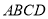 的对角线
的对角线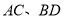 交于点
交于点 ,直角三角形
,直角三角形 绕点
绕点 按逆时针旋转,
按逆时针旋转,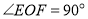
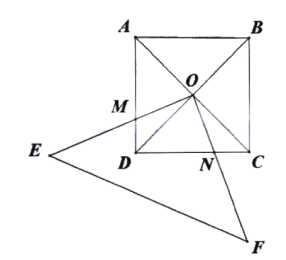
(1)若直角三角形绕点
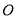 逆时针转动过程中分别交
逆时针转动过程中分别交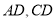 两边于
两边于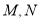 两点
两点①求证:
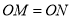 ;
;②连接
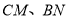 ,那么
,那么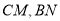 有什么样的关系?试说明理由
有什么样的关系?试说明理由(2)若正方形的边长为2,则正方形
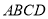 与
与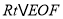 两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
两个图形重叠部分的面积为多少?(不需写过程直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

-
科目: 来源: 题型:
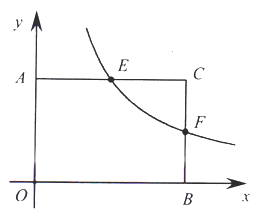
查看答案和解析>>【题目】如图,在平面直角坐标系中,
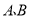 两点分别是
两点分别是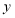 轴和
轴和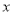 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点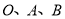 为顶点的矩形
为顶点的矩形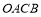 的面积为24,反比例函数
的面积为24,反比例函数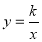 (
(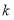 为常数且
为常数且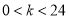 )的图象与矩形
)的图象与矩形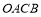 的两边
的两边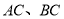 分别交于点
分别交于点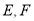 .
.
(1)若
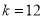 且点
且点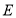 的横坐标为3.
的横坐标为3.①点
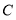 的坐标为 ,点
的坐标为 ,点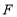 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);②在
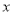 轴上是否存在点
轴上是否存在点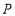 ,使
,使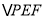 的周长最小?若存在,请求出
的周长最小?若存在,请求出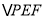 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.(2)连接
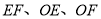 ,在点
,在点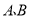 的运动过程中,
的运动过程中,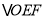 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含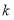 的代数式表示出
的代数式表示出 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA=6,OC=2,一条动直线l分别与BC、OA将于点E、F,且将矩形OABC分为面积相等的两部分,则点O到动直线l的距离的最大值为_____.
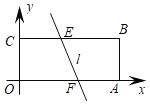
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强想利用树影测树高,他在某一时刻测得直立的标杆长0.8m,其影长为1m,同时测树影时因树靠近某建筑物,影子不全落在地上,有一部分落在墙上如图,若此时树在地面上的影长为5.5m,在墙上的影长为1.5m,求树高

相关试题

