【题目】如图,在平面直角坐标系中,![]() 两点分别是
两点分别是![]() 轴和
轴和![]() 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点![]() 为顶点的矩形
为顶点的矩形![]() 的面积为24,反比例函数
的面积为24,反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象与矩形
)的图象与矩形![]() 的两边
的两边![]() 分别交于点
分别交于点![]() .
.
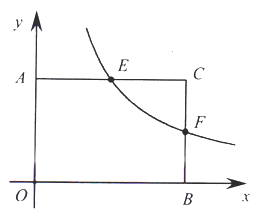
(1)若![]() 且点
且点![]() 的横坐标为3.
的横坐标为3.
①点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);
②在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,请求出
的周长最小?若存在,请求出![]() 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.
(2)连接![]() ,在点
,在点![]() 的运动过程中,
的运动过程中,![]() 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含![]() 的代数式表示出
的代数式表示出![]() 的面积.
的面积.
参考答案:
【答案】(1)①点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;②存在,周长
;②存在,周长![]() ;
;
(2)不变,![]() 的面积为
的面积为![]()
【解析】
(1)①求出点E的坐标,得出C点的纵坐标,根据面积为24即可求出C的坐标,得出F点横坐标即可求解;
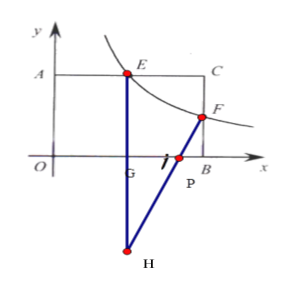
②作点E关于x轴的对称点G,连接GF,与x轴的交点为p,此时![]() 的周长最小
的周长最小
(2)先算出三角形![]() 与三角形
与三角形![]() 的面积,再求出三角形
的面积,再求出三角形![]() 的面积即可.
的面积即可.
(1)①点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;
;
②作点E关于x轴的对称点G,连接GF,求与x轴的交点为p,此时![]() 的周长最小
的周长最小
由①得EF=![]()
由对称可得EP=PH,
由 H(3,-4) F(6,2)可得HF=3![]()
△PEF=EP+PF+EF=FH+EF=![]()
(2)不变,求出三角形![]() 与三角形
与三角形![]() 的面积为
的面积为![]()
求出三角形![]() 的面积为
的面积为![]()
求出三角形![]() 的面积为
的面积为![]()
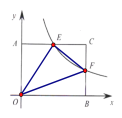
设E位(a, ![]() ),则S△AEO=
),则S△AEO=![]() ,同理可得S△AFB=
,同理可得S△AFB=![]() ,
,
∵矩形![]() 的面积为24
的面积为24
F(![]() ,
,![]() ),C(
),C(![]() ,
,![]() )
)
S△CEF=![]()
![]()
S![]() =24-
=24-![]() -k=
-k=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

-
科目: 来源: 题型:
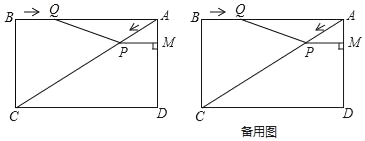
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA=6,OC=2,一条动直线l分别与BC、OA将于点E、F,且将矩形OABC分为面积相等的两部分,则点O到动直线l的距离的最大值为_____.
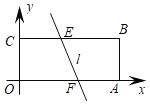
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强想利用树影测树高,他在某一时刻测得直立的标杆长0.8m,其影长为1m,同时测树影时因树靠近某建筑物,影子不全落在地上,有一部分落在墙上如图,若此时树在地面上的影长为5.5m,在墙上的影长为1.5m,求树高

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
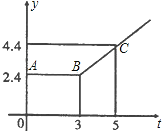
(1)写出y与t之间的函数关系式.
(2)通话2分钟应付通话费多少元?
(3)通话7分钟呢?
相关试题

