【题目】如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2. 
(1)若DG=6,求AE的长;
(2)若DG=2,求证:四边形EFGH是正方形.
参考答案:
【答案】
(1)解:∵AD=6,AH=2
∴DH=AD﹣AH=4
∵四边形ABCD是矩形
∴∠A=∠D=90°
∴在Rt△DHG中,HG2=DH2+DG2
在Rt△AEH中,HE2=AH2+AE2
∵四边形EFGH是菱形
∴HG=HE
∴DH2+DG2=AH2+AE2
即42+62=22+AE2
∴AE= ![]() =4
=4 ![]()
(2)证明:∵AH=2,DG=2,
∴AH=DG,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△DHG和Rt△AEH中,
![]() ,
,
∴Rt△DHG≌Rt△AEH(HL),
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∵四边形EFGH是菱形,
∴四边形EFGH是正方形
【解析】(1)先根据矩形的性质,利用勾股定理列出表达式:HG2=DH2+DG2 , HE2=AH2+AE2 , 再根据菱形的性质,得到等式DH2+DG2=AH2+AE2 , 最后计算AE的长;(2)先根据已知条件,用HL判定Rt△DHG≌Rt△AEH,得到∠DHG=∠AEH,因为∠AEH+∠AHE=90°,∠DHG+∠AHE=90°,可得菱形的一个角为90°,进而判定该菱形为正方形.
【考点精析】掌握菱形的性质和矩形的性质是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是ABCD的对角线,∠BAC=∠DAC.

(1)求证:AB=BC;
(2)若AB=2,AC=2 ,求ABCD的面积.
,求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
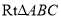 中,
中, .(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
.(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)①作
 的垂直平分线,交
的垂直平分线,交 于点
于点 ,交
,交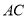 于点
于点 ;
;②以
 为圆心,
为圆心, 为半径作圆,交
为半径作圆,交 的延长线于点
的延长线于点 .
.⑵在⑴所作的图形中,解答下列问题.
①点
 与
与 的位置关系是_____________;(直接写出答案)
的位置关系是_____________;(直接写出答案)②若
 ,
, ,求
,求 的半径.
的半径.
-
科目: 来源: 题型:
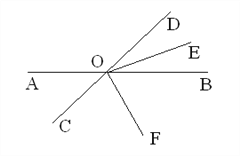
查看答案和解析>>【题目】.如图,直线AB,CD相交于点O ,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠AOF的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式3(x﹣1)≥x+1的解集是( )
A.x≤﹣2B.x≤﹣1C.x≥1D.x≥2
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长是3和7,则这个三角形的周长等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式x+2y的值是3,则代数式2x+4y+1的值是( )
A.7
B.4
C.1
D.不能确定
相关试题

