搜索
【题目】（1）①如图1，已知
，
，可得
__________.
②如图2，在①的条件下，如果
平分
，则
__________.
③如图3，在①、②的条件下，如果
，则
__________.
（2）尝试解决下面问题：已知如图4，，
，
是
的平分线，，求
的度数.
参考答案：
【答案】（1）①
，②
，③；（2）
.
【解析】
(1) ①根据两直线平行,内错角相等即可求解;
②根据角平分线的定义求解即可;
③根据互余的两个角的和等于90°,计算即可;
(2)先根据两直线平行,同旁内角互补和角平分线的定义求出∠BCN的度数,再利用互余的两个角的和等于90°即可求出.
解：(1)①由两直线平行，内错角相等得到∠BCD=60°；
②如果
平分
，则
=30°；
③如果
，则
90°－60°．
(2)、∵
，
∴
，
∵
，
∴
．
∵
是
的平分线，
∴
∵，
∴
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】雷达二维平面定位的主要原理是：测量目标的两个信息―距离和角度，目标的表示方法为
，其中，m表示目标与探测器的距离；
表示以正东为始边，逆时针旋转后的角度．如图，雷达探测器显示在点A，B，C处有目标出现，其中，目标A的位置表示为
，目标C的位置表示为
．用这种方法表示目标B的位置，正确的是（ ）
A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
-
科目： 来源： 题型：
查看答案和解析>>【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，一动点从原点O出发，按向上.向右.向下.向右的方向依次平移，每次移动一个单位，得到点A1(0，1)，A2(1，1)，A3(1，0)，A4(2，0)，…那么点A2016的坐标为________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一元二次方程ax2+bx+c=0（a≠0）中，下列说法：
①若a+b+c=0，则b2﹣4ac＞0；
②若方程两根为﹣1和2，则2a+c=0；
③若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；
④若b=2a+c，则方程有两个不相等的实根．其中正确的有（ ）
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD平分∠BAC，点P为线段AD上的一个动点，PE⊥AD交BC的延长线于点E．
（1）若∠B=35°，∠ACB=85°，求∠E得度数．
（2）当点P在线段AD上运动时，设∠B=α，∠ACB=β（β＞α），求∠E得大小．（用含α、β的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在□ABCD中，E为BC的中点，过点E作EF⊥AB于点F，延长DC，交FE的延长线于点G，连结DF，已知∠FDG=45°
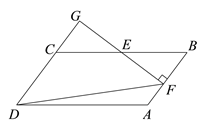
（1）求证：GD=GF.
（2）已知BC=10，
.求 CD的长.
相关试题
