搜索
【题目】小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）试验，他们共做了60次试验，试验的结果如下：
（1）计算“3点朝上”的频率和“5点朝上”的频率.
（2）小颖说：“根据上述试验，一次试验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗？为什么？
参考答案：
【答案】（1）“3点朝上”的频率是
；“5点朝上”的频率是
.（2）小颖的说法是错误的. 小红的说法也是错误的.
【解析】试题分析：根据表格中的数字概率
试题解析：（1）、“3点朝上”的频率是
；“5点朝上”的频率是
.
（2）、小颖的说法是错误的.因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大，
只有当试验的次数足够大时，该事件发生的频率稳定在事件发生的概率附近.
小红的说法也是错误的.因为事件的发生具有随机性，所以“6点朝上”的次数不一定是100次.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某手机销售商分别以每部进价分别为800元、670元的A、B两种型号的手机，下表是近两周的销售情况：
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
6台
7650元
第二周
4台
10台
11800元
（进价、售价均保持不变，利润=销售收入﹣进货成本）
（1)求A、B两种型号的手机的销售单价；
（2)若手机销售商准备再采购这两种型号的手机共30台，且利润不低于4000元，求A种型号的手机至少要采购多少台？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数y＝
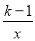（k＜0）与一次函数y＝kx＋b相交于A、B两点，若点A的坐标为（－1，7）．（1）求反比例函数和一次函数的解析式；
（2）求△ABO的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球与黄球，怎样估算不同颜色球的数量？
操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球实验，摸球实验的要求：先搅拌均匀，每次摸出一个球，记录球的颜色，放回盒中，然后重复上述过程。
活动结果：摸球实验活动一共做了50次，统计结果如下表：
推测计算：由上述的摸球实验可推算：
（1）盒中红球、黄球各占总球数的百分比分别是多少？
（2）盒中有红球多少个？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=50°，∠ACB=60°，点E在BC的延长线上，∠ABC的平分线BD与∠ACE的平分线CD相交于点D，连接AD，下列结论中不正确的是（ ）
A. ∠BAC=70° B. ∠DOC=90° C. ∠BDC=35° D. ∠DAC=55°
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球试验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据：
(1)请估计：当n很大时，摸到白球的概率约为______；(精确到0.1)
(2)估算盒子里有白球________个；
(3)若向盒子里再放入x个除颜色以外其他完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在50%，请推测x的值最有可能是多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（ ）
A. ∠1＝∠2＋∠A B. ∠1＝2∠A＋∠2
C. ∠1＝2∠2＋2∠A D. 2∠1＝∠2＋∠A
相关试题
