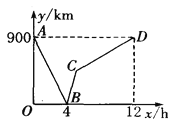
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x h,两车之间的距离为y km,如图所示的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为_______km;
(2)请解释图中点B的实际意义;
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
参考答案:
【答案】900
【解析】试题分析:
(1)由图可知,两车出发前,相距900km,即甲、乙两地相距900km;
(2)由图可知,点B的横坐标为4,纵坐标为0,说明在行驶4小时后,两车相遇了;
(3)由图可知,慢车12小时行驶了900km,由此可求得慢车的速度;再结合两车4小时共行驶了900km,可求得快车的速度;
(4)由图和题意可知,点C的横坐标是快车到达乙地的时间,点C的纵坐标是快车到达乙地时,慢车行驶的路程,由此可求得点C的坐标,结合点B的坐标即可求得线段BC的解析式及自变量的取值范围.
试题解析:
(1)由图可知,两车出发前,相距900km,
∴甲、乙两地相距900km;
(2)图中点B的实际意义是:当慢车行驶4h时,慢车和快车相遇;
(3)由图可知,慢车12h行驶的路程为900km,
∴慢车的速度为![]() (km/h);
(km/h);
∵当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,
∴慢车和快车行驶的速度之和为![]() (km/h),
(km/h),
∴快车的速度为![]() (km/h);
(km/h);
(4)根据题意,快车行驶900km到达乙地,
∴快车行驶![]() (小时)到达乙地,此时两车之间的距离为6×75=450(km),
(小时)到达乙地,此时两车之间的距离为6×75=450(km),
∴点C的坐标为(6,450).
设线段BC所表示的y与x之间的函数关系式为y=kx+b,把(4,0),(6,450)代入得
![]() ,
,
解得![]() ,
,
∴线段BC所表示的y与x之间的函数关系式为:y=225x-900,自变量x的取值范围是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=
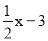 的图象是直线l1, ,l1与y轴相交于点A,与x轴相交于点B,直线l2经过点B,并且与y轴相交于点C,点C到原点的距离是6个单位长度。
的图象是直线l1, ,l1与y轴相交于点A,与x轴相交于点B,直线l2经过点B,并且与y轴相交于点C,点C到原点的距离是6个单位长度。(1)求直线l2所对应的一次函数表达式;
(2)求△ABC形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合),通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于点E,延长EG 交CD于点F.如图①,当点H与点C重合时,易证得FG=FD(不要求证明);如图②,当点H为边CD上任意一点时,求证:FG=FD.
【应用】在图②中,已知AB=5,BE=3,则FD= ,△EFC的面积为 .(直接写结果)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%。设把x公顷旱地改为林地,则可列方程( ).
A.54-x=20%×108
B.54-x=20%(108+x)
C.54+x=20%×162
D.108-x=20%(54+x) -
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α=30°,则∠α的补角是( )
A.30°
B.60°
C.120°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组从小到大的数据:0,4,x,10的中位数是5,则x=( )
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
相关试题

