【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.
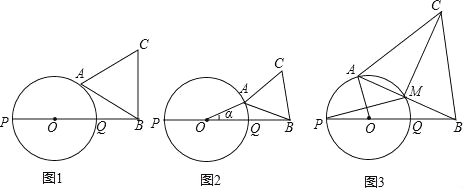
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
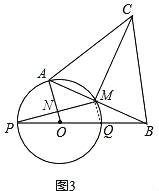
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
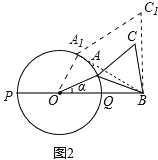
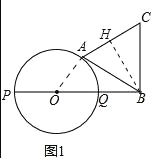
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).
参考答案:
【答案】(1)![]() ;(2)0°≤α≤60°;(3)
;(2)0°≤α≤60°;(3)![]() .
.
【解析】
试题分析:(1)连接OA,过点B作BH⊥AC,垂足为H,如图1所示.∵AB与⊙O相切于点A,∴OA⊥AB.∴∠OAB=90°.∵OQ=QB=1,∴OA=1.∴AB=![]() =
=![]() =
=![]() .∵△ABC是等边三角形,∴AC=AB=
.∵△ABC是等边三角形,∴AC=AB=![]() ,∠CAB=60°.∵sin∠HAB=
,∠CAB=60°.∵sin∠HAB=![]() ,∴HB=ABsin∠HAB=
,∴HB=ABsin∠HAB=![]() ×
×![]() =
=![]() .∴S△ABC=
.∴S△ABC=![]() ACBH=
ACBH=![]() ×
×![]() ×
×![]() =
=![]() .∴△ABC的面积为
.∴△ABC的面积为![]() .
.
(2)①当点A与点Q重合时,线段AB与圆O只有一个公共点,此时α=0°;
②当线段A1B所在的直线与圆O相切时,如图2所示,线段A1B与圆O只有一个公共点,此时OA1⊥BA1,OA1=1,OB=2,∴cos∠A1OB=![]() =
=![]() .∴∠A1OB=60°.∴当线段AB与圆O只有一个公共点(即A点)时,α的范围为:0°≤α≤60°.
.∴∠A1OB=60°.∴当线段AB与圆O只有一个公共点(即A点)时,α的范围为:0°≤α≤60°.
(3)连接MQ,如图3所示.∵PQ是⊙O的直径,∴∠PMQ=90°.∵OA⊥PM,∴∠PNO=90°.
∴∠PNO=∠PMQ.∴ON∥MQ.∴△PNO∽△PMQ.∴![]() =
=![]() =
=![]() ,∵PO=OQ=
,∵PO=OQ=![]() PQ.∴PN=
PQ.∴PN=![]() PM,ON=
PM,ON=![]() MQ.同理:MQ=
MQ.同理:MQ=![]() AO,BM=
AO,BM=![]() AB.∵AO=1,∴MQ=
AB.∵AO=1,∴MQ=![]() .∴ON=
.∴ON=![]() .∵∠PNO=90°,PO=1,ON=
.∵∠PNO=90°,PO=1,ON=![]() ,∴PN=
,∴PN=![]() .∴PM=
.∴PM=![]() .∴NM=
.∴NM=![]() .∵∠ANM=90°,AN=A0﹣ON=
.∵∠ANM=90°,AN=A0﹣ON=![]() ,∴AM=
,∴AM=![]() =
=![]() =
=![]() .∵△ABC是等边三角形,∴AC=AB=BC,∠CAB=60°.∵BM=
.∵△ABC是等边三角形,∴AC=AB=BC,∠CAB=60°.∵BM=![]() AB,∴AM=BM.∴CM⊥AB.∵AM=
AB,∴AM=BM.∴CM⊥AB.∵AM=![]() ,∴BM=
,∴BM=![]() ,AB=
,AB=![]() .∴AC=
.∴AC=![]() .∴CM=
.∴CM=![]() =
=![]() =
=![]() .∴CM的长度为
.∴CM的长度为![]() .
.
-
科目: 来源: 题型:
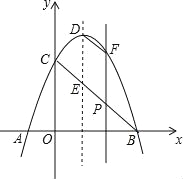
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.
(1)求此抛物线所对应的函数表达式.
(2)求PF的长度,用含m的代数式表示.
(3)当四边形PEDF为平行四边形时,求m的值.
-
科目: 来源: 题型:
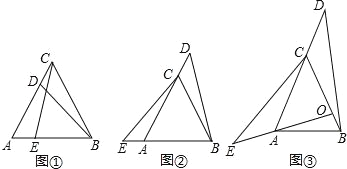
查看答案和解析>>【题目】感知:如图①,在等边三角形ABC中,点D、E分别在边AC、AB上,若AE=CD,易知△ACE≌△CBD.
探究:若图①中的点D、E分别在边AC、BA的延长线上时,如图②,△ACE与△CBD是否仍然全等?如果全等,请证明:如果不全等,请说明理由.
应用:若图②中的等边三角形ABC为等腰三角形,且AC=BC,点O是AC边的垂直平分线与BC的交点,点D、E分别在AC、OA的延长线上,如图③,若AE=CD,∠ACB=α,∠ADB=β,则∠ACE的大小为 (用含α和β的代数式表示).
-
科目: 来源: 题型:
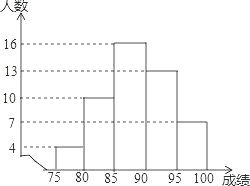
查看答案和解析>>【题目】为了了解某校全体学生参加消防知识竞赛的成绩(均为整数),从中抽取了10%的学生竞赛成绩,整理后绘制如下的频数分布直方图,其中,每组可含量最低值,不含最高值.
根据统计图提供的信息,解答下列问题:
(1)求参加消防知识竞赛的学生总人数.
(2)求抽取的部分学生中竞赛成绩在85~90的频率.
(3)如果竞赛成绩在90分以上(含90分)的同学可以获得奖励,请估计该校全体学生中获得奖励的人数.
-
科目: 来源: 题型:
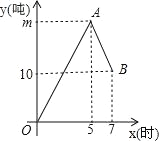
查看答案和解析>>【题目】某仓库有甲、乙、丙三辆运货车,在满载的情况下,甲车每小时可运货6吨,乙车每小时可运货10吨,某天只有乙车负责进货,甲车和丙车负责出货.如图是从早晨上班开始库存量y(吨)与时间x(时)之间的函数图象,OA段表示甲、乙两车一起工作,AB段表示乙、丙两车一起工作,且在工作期间,每辆车都是满载的.
(1)m= .
(2)在满载的情况下,丙车每小时可运货 吨.
(3)求AB段中库存量y(吨)与时间x(时)之间的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内点(2,5)关于直线x=1对称的点的坐标为( )
A.(0,5)
B.(1,4)
C.(-2,-5)
D.(2,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由小亮家向东走20m,再向北走10m就到了小丽家,若再向北走30m就到了
小红家,再向东走40m,就到了小涛家.若用(0,0)表示小亮家的位置,用(2,1)表
示小丽家的位置.
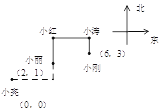
(1)小红、小涛家如何表示?
(2)小刚家的位置是(6,3),则小涛到小刚家怎么走?
相关试题

