Question

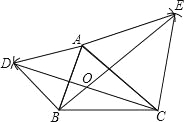
【题目】以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形，并证明：BE=CD．（尺规作图，不写作法，保留作图痕迹）

Answer 1

【答案】作图与证明见解析

【解析】

试题分析：分别以A、B为圆心，AB长为半径画弧，两弧交于点D，连接AD，BD，同理连接AE，CE，如图所示，由三角形ABD与三角形ACE都是等边三角形，得到三对边相等，两个角相等，都为60度，利用等式的性质得到夹角相等，利用SAS得到三角形CAD与三角形EAB全等，利用全等三角形的对应边相等即可得证．

试题解析：如图所示：

∵△ABD和△ACE都是等边三角形，

∴AD=AB，AC=AE，∠BAD=∠CAE=60°，

∴∠BAD+∠BAC=∠CAE+∠BAC，即∠CAD=∠EAB，

∵在△CAD和△EAB中，

，

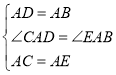∴△CAD≌△EAB（SAS），

∴BE=CD．